To maintain an electric current in a conductor for a long time, it is necessary that the charges delivered by the current are constantly removed from the end of the conductor, which has a lower potential (consider that current carriers are assumed to be positive charges), while charges are constantly supplied to the end with a higher potential. That is, it is necessary to ensure the circulation of charges. In this cycle, charges must move along a closed path. The movement of current carriers is realized using forces of non-electrostatic origin. Such forces are called third parties. It turns out that to maintain the current, external forces are needed that act along the entire length of the circuit or in individual sections of the circuit.
Definition and formula of EMF
Definition
A scalar physical quantity that is equal to the work of external forces to move a unit positive charge is called electromotive force (EMF)
, acting in a circuit or section of a circuit.
EMF is denoted by $\varepsilon$ . Mathematically, we write the definition of EMF as: $$\varepsilon=\frac{A}{q}(1)$$
where A is the work of external forces, q is the charge on which the work is performed.
The electromotive force of the source is numerically equal to the potential difference at the ends of the element if it is open, which makes it possible to measure the EMF by voltage.
The EMF that acts in a closed circuit can be defined as the circulation of the tension vector of external forces:
$$\varepsilon=\oint_{L} \bar{E}^{*} d \bar{l}(2)$$
where $\bar{E}^{*}$ is the field strength of external forces. If the field strength of external forces is not zero only in part of the circuit, for example, on segment 1-2, then integration in expression (2) can be carried out only over this section. Accordingly, the EMF acting on circuit section 1-2 is defined as:
$$\varepsilon=\int_{1}^{2} \bar{E}^{*} d \bar{l}(3)$$
Formula (2) gives the most general definition of EMF, which can be used for any cases.
From electrostatics to electrokinetics
Between the end of the 18th and the beginning of the 19th century, the work of scientists such as Coulomb, Lagrange and Poisson laid the mathematical foundations for the determination of electrostatic quantities. Progress in the understanding of electricity at this historical stage is obvious. Franklin had already introduced the concept of “amount of electrical substance,” but so far neither he nor his successors have been able to measure it.
Following Galvani's experiments, Volta tried to find evidence that the animal's "galvanic fluids" were of the same nature as static electricity. In his search for truth, he discovered that when two electrodes of different metals come into contact through an electrolyte, both become charged and remain charged despite the circuit being closed by the load. This phenomenon did not correspond to existing ideas about electricity because electrostatic charges in such a case had to recombine.
Volta introduced a new definition of the force acting in the direction of separating charges and maintaining them in this state. He called it electromotive. Such an explanation for the description of battery operation did not fit into the theoretical foundations of physics at that time. In the Coulomb paradigm of the first third of the 19th century. d.s. Volta was determined by the ability of some bodies to generate electricity in others.
Ohm made the most important contribution to the explanation of the operation of electrical circuits. The results of a series of experiments led him to the construction of the theory of electrical conductivity. He introduced the quantity “voltage” and defined it as the potential difference across the contacts. Like Fourier, who in his theory distinguished between the amount of heat and temperature in heat transfer, Ohm created a model by analogy relating the amount of charge transferred, voltage and electrical conductivity. Ohm's law did not contradict the accumulated knowledge of electrostatic electricity.
You might be interested in: Design and use of a resistor in an electrical circuit
Then, thanks to Maxwell and Faraday, explanatory models of current received a new field theory. This allowed the development of a field-related energy concept for both static potentials and electromotive force. The main dates for the evolution of the concept of EMF:
- 1800 - creation of the Voltaic galvanic battery;
- 1826 - Ohm formulates his law for a complete chain;
- 1831 - discovery of electromagnetic induction by Faraday.
Ohm's law for an arbitrary section of a circuit
The section of the chain on which external forces act is called heterogeneous. It satisfies the following equality:
$$U_{12}=\varphi_{1}-\varphi_{2}+\varepsilon_{12}(4)$$
where U12=IR21 – voltage drop (or voltage) in circuit section 1-2 (I-current); $\varphi_{1}-\varphi_{2}$ – potential difference between the ends of the section; $\varepsilon_12$ is the electromotive force contained in the circuit section. $\varepsilon_12$ is equal to the algebraic sum of the emf of all sources that are located in a given area.
It should be taken into account that EMF can be positive and negative. The EMF is called positive if it increases the potential in the direction of the current (the current flows from the minus to the plus of the source).
Definition and physical meaning
Applying some potential difference between the two ends of a conductor will create a flow of electrons from one end to the other. But this is not enough to maintain the flow of charges in the conductor. The drift of electrons leads to a decrease in the potential until it balances (the current stops). Thus, to create a direct current, mechanisms are needed that continuously return the described system to its original configuration, that is, preventing the aggregation of charges as a result of their movement. For this purpose, special devices called power supplies are used.
To illustrate their operation, it is convenient to consider a closed loop of resistance and a galvanic power source (battery). If we assume that there is no current inside the battery, then the described problem of combining charges remains unresolved. But in a circuit with a real power source, electrons are constantly moving. This occurs due to the fact that the flow of ions also flows inside the battery from the negative electrode to the positive one. The energy source that moves these charges in the battery is chemical reactions. This energy is called electromotive force.
EMF is a characteristic of any energy source capable of controlling the movement of electrical charges in a circuit. In analogy with a closed hydraulic circuit, the work of the energy source. d.s. corresponds to the operation of the pump to create water pressure. Therefore, the symbol representing these devices is indistinguishable on hydraulic and electrical diagrams.
Despite the name, electromotive force is not actually a force and is measured in volts. Its numerical value is equal to the work done to move a charge along a closed circuit. The source emf is expressed by the formula E=A/q , in which:
- E—electromotive force in volts;
- A is the work of external forces to move the charge in joules;
- q is the displaced charge in coulombs.
From this EMF formula it follows that the electromotive force is not a property of the circuit or load, but is the ability of the electricity generator to separate charges.
Comparison with potential difference
Electromotive force and potential difference in a circuit are very similar physical quantities, since both are measured in volts and are determined by the work done to move a charge. One of the main semantic differences is that e. d.s. (E) is caused by converting some energy into electrical energy, while potential difference (U) converts electrical energy into other forms. Other differences look like this:
- E transfers energy to the entire circuit. U is a measure of the energy between two points on a diagram.
- E causes U, but not vice versa.
- E is induced in electric, magnetic and gravitational fields.
- Concept e. d.s. is applicable only to the electric field, while potential difference is applicable to magnetic, gravitational and electric fields.
You might be interested in the principle of operation and application of a controlled thyristor
The voltage at the power supply terminals is usually different from the source emf. This occurs due to the presence of internal resistance of the source (electrolyte and electrodes, generator windings). The formula connecting the potential difference and the emf of the current source looks like U=E-Ir. In this expression:
- U is the voltage at the source terminals;
- r is the internal resistance of the source;
- I is the current in the circuit.
From this formula for electromotive force it follows that e. d.s. equal to the voltage when no current flows in the circuit. An ideal EMF source creates a potential difference regardless of the load (flowing current) and has no internal resistance.
In nature, there cannot be a source with infinite power when shorted across the terminals, just like a material with infinite conductivity. The ideal source is used as an abstract mathematical model.
Example of outside forces
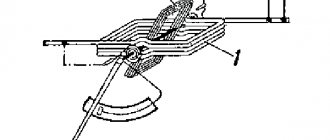
The simplest diagram of a source of external force (current source), which is of mechanical origin, is shown in Fig. 1.
Figure 1. Diagram of a third-party force source. Author24 - online exchange of student work
Do you need proofreading or review of academic work? Ask a question to the teacher and get an answer in 15 minutes! Ask a Question
Let there be an electrically neutral medium with equal charges of opposite sign between electrodes A and B (Fig. 1). An external force of non-electrical origin moves positive charges to electrode B (this electrode is positively charged), and negative charges to electrode A (negatively charged electrode). An electric current flows in an external circuit. Current produces work. The energy that is necessary to produce such work is supplied by external forces, which spend it on separating charges between the electrodes. The current inside the external power source short-circuits the current in the external circuit. The direction of the electric current in the external circuit is from the positive electrode to the negative, and vice versa inside the current source. A practical implementation of such a scheme is an electrostatic machine.
The essence of outside forces
In order for a current to exist in a conductor for a long time, it is necessary that the movement of charged particles, for example, electrons, be supported by some external force.
Therefore, it is necessary that the charges brought there are continuously removed from the end of the conductor with a lower potential (we assume that the electric current carriers are positive), and charges are constantly supplied to the end with a higher potential. That is, a circulation of charges along a closed path is necessary, then the current will flow. This fact is consistent with the closedness of the current lines. That is, EMF is the work done to move a positive charge in a closed circuit. Note 1
An external electromotive force (hereinafter referred to as an external force) cannot be electrostatic, because the electrostatic field is potential.
Finished works on a similar topic
Course work Third-party forces and EMF 430 ₽ Abstract Third-party forces and EMF 260 ₽ Test work Third-party forces and EMF 210 ₽
Receive completed work or specialist advice on your educational project Find out the cost
The work done by potential force for a current-carrying circuit is zero. Under this condition, the current cannot exist, since the current must do work to overcome the resistance of the conductors. An external force can be mechanical or electrical (not electrostatic), of chemical origin, etc. Also, for a closed circuit, the cause of the occurrence of EMF can be a change in the magnetic field flow, this is due to the phenomenon of electromagnetic induction.
Taking into account external forces, Ohm’s law in local form is written as:
$\overrightarrow{j}=\sigma \left(\overrightarrow{E}+\overrightarrow{E_{stor}}\right)\left(1\right)$, where:
- $\overrightarrow{j}$ is the electric current density vector,
- $\sigma$ — specific conductivity,
- $\overrightarrow{E}$ is the field strength of Coulomb forces, $\overrightarrow{E_{stor}}$ is the field strength of external forces.
A simple explanation of electromotive force
Let's assume that our village has a water tower. It is completely filled with water. Let's assume that this is an ordinary battery. The tower is a battery!
All the water will put strong pressure on the bottom of our turret. But it will be strong only when this structure is completely filled with H2O.
As a result, the less water, the weaker the pressure will be and the less pressure of the stream. Having opened the tap, we will notice that every minute the range of the jet will decrease.
As a result:
- Tension is the force with which water presses on the bottom. That is pressure.
- Zero voltage is the bottom of the tower.
Everything is the same with the battery.
First of all, we connect the energy source to the circuit. And we close it accordingly. For example, we insert the battery into a flashlight and turn it on. Initially, we will notice that the device burns brightly. After some time, its brightness will noticeably decrease. That is, the electromotive force decreased (it leaked out compared to water in the tower).
If we take a water tower as an example, then the EMF is a pump constantly pumping water into the tower. And it never ends there.