What is resonance?
Definition of the phenomenon by TOE: electrical resonance occurs in an electrical circuit at a certain resonant frequency, when some parts of the resistance or conductivity of the circuit elements cancel each other. In some circuits, this occurs when the impedance between the input and output of the circuit is almost zero and the signal transfer function is close to unity. In this case, the quality factor of this circuit is very important.
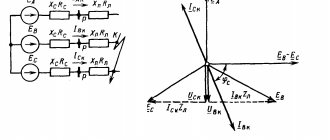
Connection of two branches at resonance
Signs of resonance:
- The components of the reactive branches of the current are equal to each other IPC = IPL, antiphase is formed only when the net active energy at the input is equal;
- The current in individual branches exceeds the entire current of a particular circuit, while the branches are in phase.
In other words, resonance in an AC circuit implies a special frequency, and is determined by the values of resistance, capacitance and inductance. There are two types of current resonance:
- Consistent;
- Parallel.
For series resonance, the condition is simple and is characterized by minimal resistance and zero phase, it is used in reactive circuits, and it is also used in branched circuits. Parallel resonance or the concept of an RLC circuit occurs when the inductive and capacitive inputs are equal in magnitude but cancel each other out since they are at an angle of 180 degrees from each other. This connection must be constantly equal to the specified value. It has received wider practical application. The sharp minimum impedance that it exhibits is beneficial for many electrical household appliances. The sharpness of the minimum depends on the resistance value.
An RLC circuit (or circuit) is an electrical circuit that consists of a resistor, inductor, and capacitor connected in series or parallel. The RLC parallel oscillating circuit gets its name from the abbreviation of the physical quantities representing resistance, inductance and capacitance, respectively. The circuit forms a harmonic oscillator for the current. Any oscillation of the current induced in the circuit fades over time if the movement of the directed particles is stopped by the source. This resistor effect is called attenuation. The presence of resistance also reduces the peak resonant frequency. Some resistance is unavoidable in real circuits, even if a resistor is not included in the circuit.
Resonance is a mode of operation of a circuit that includes inductive and capacitive elements in which its input resistance (input conductance) is real. The consequence of this is that the current at the input of the circuit is in phase with the input voltage.
Resonance in a circuit with elements connected in series (voltage resonance)
For the circuit in Fig. 1, we have
Where
| ; | (1) |
| . | (2) |
Depending on the ratio of the quantities and, three different cases are possible.
1. Inductance predominates in the circuit, i.e. , and consequently,
. This mode corresponds to the vector diagram in Fig. 2, a.
2. Capacitance predominates in the circuit, i.e. , which means . This case is reflected in the vector diagram in Fig. 2, b.
3. - case of voltage resonance (Fig. 2,c).
Voltage resonance condition
| . | (3) |
Moreover, as follows from (1) and (2), .
At voltage resonance or modes close to it, the current in the circuit increases sharply. In the theoretical case, at R=0 its value tends to infinity. According to the increase in current, the voltages on the inductive and capacitive elements increase, which can be many times higher than the voltage of the power source.
Let, for example, in the circuit in Fig. 1 . Then , and, accordingly, .
The phenomenon of resonance finds useful application in practice, in particular in radio engineering. However, if it occurs spontaneously, it can lead to emergency conditions due to the appearance of large overvoltages and overcurrents.
The physical essence of resonance lies in the periodic exchange of energy between the magnetic field of the inductor and the electric field of the capacitor, and the sum of the field energies remains constant.
The essence of the matter does not change if there are several inductive and capacitive elements in the circuit. Indeed, in this case, and relation (3) is satisfied for equivalent values of LE and SE.
As analysis of equation (3) shows, the resonance mode can be achieved by changing the parameters L and C, as well as the frequency. Based on (3), for the resonant frequency we can write
| . | (4) |
Resonance curves
are called the dependences of current and voltage on frequency. As an example, in Fig. 3 shows typical I(f) curves; and for the circuit in Fig. 1 at U=const.
An important characteristic of a resonant circuit is the quality factor
Q, determined by the ratio of the voltage on the inductive (capacitive) element to the input voltage:
| , | (5) |
— and characterizing the “selective” properties of the resonant circuit, in particular its bandwidth
.
Another parameter of the resonant circuit is the characteristic impedance
, related to the quality factor by the relation
| , | (6) |
or taking into account (4) and (5) for we can write:
| . | (7) |
Resonance in a circuit with parallel-connected elements (current resonance)
For the circuit fig. 4 we have
,
Where
| ; | (8) |
| . | (9) |
Depending on the ratio of the values and , as in the case of series connection of elements discussed above, three different cases are possible.
The circuit is dominated by inductance, i.e. , and consequently, . This mode corresponds to the vector diagram in Fig. 5, a.
The circuit is dominated by capacitance, i.e. , which means . This case is illustrated by the vector diagram in Fig. 5 B.
- case of current resonance (Fig. 5, c).
Current resonance condition or
| . | (10) |
Moreover, as follows from (8) and (9), . Thus, with current resonance, the input conductance of the circuit is minimal, and the input resistance, on the contrary, is maximum. In particular, in the absence of a circuit in Fig. 4 resistor R, its input resistance in resonance mode tends to infinity, i.e. at current resonance, the current at the input of the circuit is minimal.
The identity of relations (3) and (5) indicates that in both cases the resonant frequency is determined by relation (4). However, expression (4) should not be used for any resonant circuit. It is valid only for the simplest circuits with a series or parallel connection of inductive and capacitive elements.
When determining the resonant frequency in a circuit of arbitrary configuration or, in the general case, the ratio of circuit parameters in the resonance mode, one should proceed from the condition that the input resistance (input conductivity) of the circuit is real.
For example, for the circuit in Fig. 6 we have
Since in the resonance mode the imaginary part must be equal to zero, the resonance condition has the form
,
where, in particular, is the resonant frequency.
Resonance in a complex circuit
The resonance condition for a complex circuit with a mixed connection of several inductive and capacitive elements, which consists in the equality to zero of the imaginary part of the input resistance or input conductivity, determines the presence of equations corresponding to this condition with respect to several real roots, i.e. Such circuits correspond to several resonant frequencies.
When determining the resonant frequencies for a reactive two-terminal network, the analytical expression of its input reactance or input reactive conductance should be presented as a ratio of two polynomials in powers, i.e. or . Then the roots of the equation will give the frequency values that correspond to voltage resonances, and the roots of the equation will give the frequency values at which current resonances occur. The total number of resonant frequencies in the circuit is one less than the number of inductive and capacitive elements in the circuit obtained from the original one by reducing it to a circuit (using equivalent transformations) with a minimum number of these elements. Characteristic in this case is the fact that the modes of voltage and current resonances alternate.
As an example, let us determine the resonant frequencies for the circuit in Fig. 7. The expression for the input resistance of this circuit is
From the solution of the equation we obtain the frequency corresponding to the voltage resonance, and from the solution of the equation we obtain the frequency corresponding to the current resonance.
Literature
- Fundamentals
of circuit theory: Textbook. for universities / G.V. Zeveke, P.A. Ionkin, A.V. Netushil, S.V. Strakhov. –5th ed., revised. –M.: Energoatomizdat, 1989. -528 p. - Bessonov
L.A. Theoretical foundations of electrical engineering: Electric circuits. Textbook for students of electrical engineering, energy and instrument engineering specialties of universities. –7th ed., revised. and additional –M.: Higher. school, 1978. –528 p.
Test questions and tasks
- What is voltage resonance and how is it characterized?
- What is current resonance, how is it characterized?
- What is the physical essence of resonant modes?
- On the basis of what conditions are resonant frequencies determined in the general case?
- In the circuit in Fig. 1 R=1 Ohm; L=10 mH; C=10 µF. Determine the resonant frequency and quality factor of the circuit.
- What conditions are necessary and sufficient for the circuit in Fig. 1 the relation was fulfilled?
- Determine the resonant frequency for the circuit in Fig. 7, if capacitor C3 is replaced by resistor R3.
Answer: .
Answer: .
Application
Almost all power electrical engineering uses just such an oscillatory circuit, say, a power transformer. The circuit is also necessary for setting up the operation of a TV, capacitive generator, welding machine, radio receiver; it is used by the “matching” technology of television broadcast antennas, where you need to select a narrow frequency range of some of the waves used. The RLC circuit can be used as a band-pass filter, notch filter, for low-pass or high-pass distribution sensors.
Resonance is even used in aesthetic medicine (microcurrent therapy) and bioresonance diagnostics.
Description of the phenomenon
If in a certain electrical circuit (see Fig. 1) there are capacitive and inductive elements that have their own resonant frequencies, then when these frequencies coincide, the amplitude of the oscillations will increase sharply. That is, there is a sharp surge in stress on these elements. This can cause destruction of electrical circuit elements.
Rice. 1. Resonance in an electrical circuit
Let's look at this example to see what phenomena will occur when an alternating current generator is connected to the contacts of the circuit. Note that coils and capacitors have properties that can be compared to the analogue of a reactive resistor. In particular, a choke in an electrical circuit creates inductive reactance. The capacitor causes capacitance.
The inductive element causes a phase shift, characterized by a lag of the current from the voltage by ¼ of a period. Under the action of a capacitor, the current, on the contrary, leads the voltage by ¼ period.
In other words, the effect of inductance is opposite to the effect on the phase shift of capacitance. That is, inductors and capacitive elements influence the generator in different ways and adjust the phase relationships between electric current and voltage in their own way.
Formula
The total reactance of the elements we are considering is equal to the sum of the resistances of each of them. Taking into account the opposite actions, we can write: Xtot = XL - Xc, where XL = ωL is the inductive reactance, the expression Xc = 1/ωC is the capacitive reactance.
Figure 2 shows graphs of the dependence of the circuit impedance and the associated current on the reactance of the inductive element. Pay attention to how the total resistance decreases as the reactance RL (graph b) and how the current increases (graph c).
Rice. 2. Graphs of the dependence of current parameters on the drop in reactance
Electrical circuits consisting of series-connected capacitors, passive resistors and inductors are called series resonant (oscillatory) circuits (see Fig. 2). There are also parallel circuits in which R, L, C elements are connected in parallel (Fig. 3).
Rice. 3. Series oscillatory circuit
Rice. 4. Parallel oscillatory circuit
In resonance mode, the power of the power source will be dissipated only through active resistances (including the active resistance of the coil). Resonant circuits are characterized by losses only of active power, which is spent to maintain the oscillatory process. Reactive power on LC elements is not consumed. The current in the resonant mode takes on the maximum value:
The value of Q is usually called the term “Q factor” of the circuit. This parameter shows how many times the voltage generated at the contacts of the reactive elements exceeds the input voltage U of the electrical network. To describe the ratio of output and input voltages, the coefficient K is often used. At resonance:
Formulation
The described phenomenon is quite common in electrical engineering. Sometimes they fight it, and sometimes they specially create conditions for the formation of resonance. The main characteristics of any resonant circuit are the quality factor and frequency parameters [1].
If XL = Xc , the equality is true: ωL = 1/ωC , from here we obtain:
If ω = ω – voltage resonance occurs. The frequencies coincide when the inductive reactance is equal to the capacitive reactance of the capacitor. In such cases, only active resistance R will act in the circuit. The presence of reactive elements in the circuit leads to an increase in the total resistance of the circuit (Z):
where R is the total active resistance.
Considering that, according to Ohm's law, U = I/Z , it can be argued that the total voltage in the circuit depends, among other things, on the terms of the inductive and capacitive reactance.
If in the circuit under consideration (Fig. 1) there was no active resistance R , then the value of the total resistance Z would tend to 0. Consequently, the voltage on the reactive elements increases to a critical level.
Since XL and Xc depend on the frequency of the input voltage, for resonance to occur, you must select the appropriate network frequency, or change the parameters of the coil or capacitor until the resonant frequencies coincide. Any violation of the resonance conditions immediately leads to the system exiting the resonant mode with a subsequent voltage drop.
Conditions of attack
Resonance phenomena occur only if the following conditions are present:
- The presence of minimal active resistance in a section of the electrical circuit.
- Equality of reactances arising on the LC chain.
- Coincidence of the input frequency of the power supply with the resonant frequency of the oscillatory circuit.
When there is resonance in the circuit, the voltages on its elements can increase by an order of magnitude or more.
Principle of current resonance
We can make a resonant or oscillating circuit at its natural frequency, say, to power a capacitor, as the following diagram demonstrates:
Circuit for powering a capacitor
The switch will be responsible for the direction of vibration.
Circuit: resonant circuit switch
The capacitor stores all the current at the moment when time = 0. Oscillations in the circuit are measured using ammeters.
Scheme: the current in the resonant circuit is zero
Directed particles move to the right. The inductor receives current from the capacitor.
When the polarity of the circuit returns to its original form, the current returns to the heat exchanger.
Now the directed energy goes back into the capacitor, and the circle repeats again.
In real mixed circuit circuits there is always some resistance which causes the amplitude of the directed particles to grow smaller with each circle. After several changes in the polarity of the plates, the current decreases to 0. This process is called a damped sine wave signal. How quickly this process occurs depends on the resistance in the circuit. But the resistance does not change the frequency of the sine wave. If the resistance is high enough, the current will not fluctuate at all.
The AC designation means that the energy leaving the power supply oscillates at a specific frequency. An increase in resistance helps to reduce the maximum size of the current amplitude, but this does not lead to a change in the resonance frequency. But an eddy current process can form. After its occurrence, network interruptions are possible.
Voltage resonance
If a capacitor and an inductor are connected in series with the generator, then, provided their reactances are equal, voltage resonance will occur. In this case, the active part Z should be as small as possible.
It is worth noting that inductance and capacitance only have reactive qualities in idealized examples. In real circuits and elements, there is always active resistance of the conductors, although it is extremely small.
At resonance, energy is exchanged between the inductor and the capacitor. In ideal examples, when the energy source (generator) is initially connected, energy is stored in the capacitor (or inductor) and after it is turned off, continuous oscillations occur due to this exchange.
The voltages across the inductance and capacitance are approximately the same, according to Ohm's law:
U=I/X
Where X is Xc capacitive or XL inductive reactance, respectively.
A circuit consisting of inductance and capacitance is called an oscillatory circuit. Its frequency is calculated by the formula:
The period of oscillation is determined by the Thompson formula:
Since reactance depends on frequency, the inductance resistance increases with increasing frequency, while that of the capacitance decreases. When the resistances are equal, the total resistance is greatly reduced, as shown in the graph:
The main characteristics of the circuit are quality factor (Q) and frequency. If we consider the circuit as a four-terminal network, then its transmission coefficient after simple calculations is reduced to the quality factor:
K=Q
And the voltage at the circuit terminals increases in proportion to the transmission coefficient (quality factor) of the circuit.
Uk=Uin*Q
With voltage resonance, the higher the quality factor, the more the voltage on the circuit elements will exceed the voltage of the connected generator. The voltage can increase tens or hundreds of times. This is shown in the graph:
Power losses in the circuit are caused only by the presence of active resistance. Energy is taken from the power source only to maintain oscillations.
The power factor will be equal to:
cosФ=1
This formula shows that losses occur due to active power:
S=P/Cosф
Concept of resonance currents. Conditions for its occurrence and methods of implementation
Current resonance is a resonance that occurs in a parallel oscillating circuit when it is connected to a voltage source whose frequency coincides with the natural frequency of the circuit.
Current resonance condition: , .
B1 – reactive conductivity of the first branch,
B2 – reactive conductivity of the second branch.
A method of exciting oscillations in an electrical circuit, which consists in generating oscillations by regulating the signal that controls the excitation of oscillations.
Resonance of currents and its signs
The mode in which, in a circuit containing parallel branches with inductive and capacitive elements, the current of the unbranched section of the circuit is in phase with the voltage (φ = 0), is called current resonance.
Signs of current resonance:
The reactive components of the branch currents are equal to IPC = IPL and are in antiphase in the case when the input voltage is purely active;
The branch currents exceed the total circuit current, which has a minimum value and are in phase.
Instantaneous power of a sinusoidal current circuit
Instantaneous power is the product of the instantaneous voltage at the input of the circuit and the instantaneous current.
Let the instantaneous voltage and current be determined by the formulas:
Then
Average value of instantaneous power for the period
From the resistance triangle, a
We get another formula:
The arithmetic average of power over a period is called active power and is denoted by the letter P.
This power is measured in watts and characterizes the irreversible conversion of electrical energy into another type of energy, for example, thermal, light and mechanical energy.
Let's take a reactive element (inductance or capacitance). Active power in this element, since the voltage and current in the inductance or capacitance differ in phase by 90o. There are no irreversible losses of electrical energy in reactive elements, and the elements do not heat up.
A reversible process occurs in the form of an exchange of electrical energy between the source and the receiver. To qualitatively assess the intensity of energy exchange, the concept of reactive power Q is introduced.
Let's transform expression (6.23):
where is the instantaneous power in the active resistance;
- instantaneous power in a reactive element (in inductance or capacitance).
The maximum or peak value of power p2 is called reactive power
where x is reactance (inductive or capacitive).
Reactive power, measured in reactive volt-amperes, is spent on creating a magnetic field in an inductance or an electric field in a capacitance. The energy stored in a capacitance or inductance is periodically returned to the power source.
The amplitude value of the total power p = p1 + p2 is called the total power.
The total power, measured in volt-amperes, is equal to the product of the effective values of voltage and current:
where z is the total resistance of the circuit.
Total power characterizes the maximum capabilities of the energy source. Part of the total power can be used in an electrical circuit
where is the power factor or cosine phi.
Power factor is one of the most important characteristics of electrical devices. Special measures are taken to increase the power factor.
Active, reactive and apparent power of sinusoidal current circuits
Active power.
The unit of measurement is watt (W, W).
The average value of instantaneous power over a period T is called active power: In single-phase sinusoidal current circuits where U and I are the rms values of voltage and current, φ is the phase shift angle between them. For non-sinusoidal current circuits, the electric power is equal to the sum of the corresponding average powers of the individual harmonics. Active power characterizes the rate of irreversible conversion of electrical energy into other types of energy (thermal and electromagnetic). Active power can also be expressed in terms of current, voltage and the active component of the circuit resistance r or its conductivity g using the formula P=I2∙r=U2∙g. In any electrical circuit of both sinusoidal and non-sinusoidal current, the active power of the entire circuit is equal to the sum of the active powers of the individual parts of the circuit; for three-phase circuits, the electrical power is defined as the sum of the powers of the individual phases. The active power is related to the total power S by the relation
In the theory of long lines (analysis of electromagnetic processes in a transmission line, the length of which is comparable to the length of the electromagnetic wave), a complete analogue of active power is transmitted power, which is defined as the difference between the incident power and the reflected power.
Reactive power.
The unit of measurement is reactive volt-ampere (var).
Reactive power is a quantity characterizing the loads created in electrical devices by fluctuations in the energy of the electromagnetic field in a sinusoidal alternating current circuit, equal to the product of the rms values of voltage U and current I, multiplied by the sine of the phase shift angle φ between them: (if the current lags behind the voltage, the shift phase is considered positive, if it is ahead - negative). Reactive power is related to total power S and active power P by the ratio: .
The physical meaning of reactive power is energy pumped from the source to the reactive elements of the receiver (inductors, capacitors, motor windings), and then returned by these elements back to the source during one oscillation period, referred to this period.
It should be noted that the value of sin φ for values of φ from 0 to plus 90° is a positive value. The value of sin φ for φ values from 0 to −90° is a negative value. In accordance with the formula Q = UI sin φ, reactive power can be either a positive value (if the load is active-inductive in nature) or negative (if the load is active-capacitive in nature). This circumstance emphasizes the fact that reactive power does not participate in the operation of electric current. When a device has positive reactive power, it is customary to say that it consumes it, and when it produces negative power, it produces it, but this is purely a convention due to the fact that most power-consuming devices (for example, asynchronous motors), as well as purely active loads, are connected through a transformer, are active-inductive.
Synchronous generators installed in power plants can both produce and consume reactive power depending on the magnitude of the excitation current flowing in the generator rotor winding. Due to this feature of synchronous electrical machines, the specified network voltage level is regulated. To eliminate overloads and increase the power factor of electrical installations, reactive power compensation is carried out.
The use of modern electrical measuring transducers on microprocessor technology allows for a more accurate assessment of the amount of energy returned from an inductive and capacitive load to an alternating voltage source.
Reactive power measuring converters using the formula Q = UI sin φ are simpler and much cheaper than microprocessor-based measuring converters.
Full power.
The unit of total electrical power is volt-ampere (V A, VA)
Total power is a value equal to the product of the effective values of the periodic electric current I in the circuit and the voltage U at its terminals: S = U·I; is related to active and reactive power by the ratio: S=, where P is active power, Q is reactive power (with an inductive load Q > 0, and with a capacitive load Q < 0).
The vector relationship between total, active and reactive power is expressed by the formula:
Total power has practical significance as a value that describes the loads actually imposed by the consumer on the elements of the supply network (wires, cables, distribution boards, transformers, power lines), since these loads depend on the current consumed, and not on the energy actually used by the consumer. This is why the power rating of transformers and distribution boards is measured in volt-amperes rather than watts.