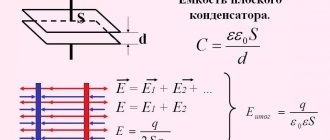
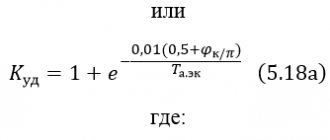Calculation of DC electromagnetic coil
Electromagnets are used in many electrical devices. It is a coil of wire wound on an iron core, the shape of which can be different. The iron core is one part of the magnetic circuit, and the other part, with the help of which the path of the magnetic lines of force is closed, is the armature. The magnetic circuit is characterized by the magnitude of magnetic induction - B
, which depends on the field strength and magnetic permeability of the material. That is why the cores of electromagnets are made of iron, which has high magnetic permeability.
When designing electromagnets, it is highly desirable to obtain a large power flux. This can be achieved by reducing the magnetic resistance. To do this, you need to select a magnetic core with the shortest path length of the power lines and the largest cross-section, and the material should be an iron material with high magnetic permeability.
Another way of increasing the power flow by increasing the ampere turns is not acceptable, since in order to save wire and power, one should strive to reduce the ampere turns.
Usually, calculations of electromagnets are made according to special schedules. To simplify the calculations, we will also use some conclusions from the graphs. Suppose it is necessary to determine the ampere-turns and power flux of a closed iron magnetic circuit, shown in Figure 4a and made of iron of the lowest quality.
Looking at the graph of iron magnetization, it is easy to see that the most advantageous magnetic induction is in the range from 10 000
up to
14,000
power lines per 1 cm2, which corresponds to from
2
to
7
ampere turns per 1 cm. To wind coils with the smallest number of turns and more economical in terms of power supply, this value must be taken for calculations (
10,000
power lines per 1 cm2 at 2 ampere turns per 1 cm length).
In this case, the calculation can be made as follows. So, with a magnetic circuit length Z=/1-)-/2
equal to
20 cm -f- 10 cm = 30 cm
,
2×30=60
ampere turns will be required.
For a two-pole magnet, this result should be doubled. Therefore, P=24.8 kg ^ 25 kg
. When determining the lifting force, it must be remembered that it depends not only on the length of the magnetic circuit, but also on the area of contact between the armature and the core. Therefore, the armature must fit exactly against the pole pieces, otherwise even the slightest air gaps will cause a strong reduction in lift.
Next, the electromagnet coil is calculated. In our example, the lifting force is 25 kg
provided by
60
ampere turns.
Let us consider by what means the product N-J—60
ampere turns can be obtained.
Obviously, this can be achieved either by using a large current with a small number of coil turns, for example 2 A and 30 turns, or by increasing the number of coil turns while reducing the current, for example 0.25 A and 240 turns. Thus, in order for an electromagnet to have a lifting force of 25 kg, both 30 turns and 240 turns can be wound on its core, but at the same time the value of the supply current can be changed. Of course, you can choose a different ratio.
However, changing the current value within large limits is not always possible, since it will necessarily require changing the diameter of the wire used. Thus, during short-term operation (several minutes) for wires with a diameter of up to 1. mm, the permissible current density at which the wire does not overheat strongly can be taken equal to 5 A/mm2
.
In our example, the wire should have the following cross-section: for a current of 2A - 0.4 mm2
, and for a current of
0.25A - 0.05 mm2
.
Which of these wires should be wound? On the one hand, the choice of wire diameter can be determined by the assortment of wire available to the manager, on the other hand, by the capabilities of the power sources in both current and voltage. Indeed, two coils, one of which is made of thick wire of 0.7 mm and with a small number of turns - 30, and the other of which is made of wire of 0.2 mm and a number of turns of 240, will have sharply different resistance.
Knowing the diameter of the wire and its length, you can easily determine the resistance. The length of the wire is equal to the product of the total number of turns and the length of one of them (average): l=Nxlt
where
lt
is the length of one turn, equal to
3.14 x
L. In our example, D = 2 cm, and 1g x 6.3 cm. Therefore, for the first coil, the wire length will be 30 x 6.3 = 190 cm, and for the second - 240 X 6.3 = 1,512 cm. The winding resistances will be also different.
Using Ohm's law, it is easy to calculate the required voltage. So, to create a current of 2A in the windings, the required voltage is 0.2V, and for a current of 0.25A - 2.5V.
Thus, to power the first coil, one element or battery is enough, and to reduce the voltage you have to turn on the rheostat; To power the second coil, you need to take two elements, connecting them in series. It is clear that in the second case there are fewer losses of electricity and the winding turns out to be more profitable.
Analysis of the results obtained allows us to draw the following conclusion: the diameter of the wire is selected so that the coil can be powered from only one element (or battery) without any rheostats, where energy is wasted involuntarily. It is easy to see that with a wire diameter of approximately 0.4 mm and a current strength of about 0.4 A, the required voltage to power the coil will be 1.3-1.4 V, that is, exactly the voltage of one element.
Source
How to calculate the power of an electromagnet
Electromagnets are used in many electrical devices. It is a coil of wire wound on an iron core, the shape of which can be different. The iron core is one part of the magnetic circuit, and the other part, with the help of which the path of the magnetic lines of force is closed, is the armature. A magnetic circuit is characterized by the magnitude of magnetic induction - V
, which depends on the field strength and magnetic permeability of the material. That is why the cores of electromagnets are made of iron, which has high magnetic permeability.
When designing electromagnets, it is highly desirable to obtain a large power flux. This can be achieved by reducing the magnetic resistance. To do this, you need to select a magnetic core with the shortest path length of the power lines and the largest cross-section, and the material should be an iron material with high magnetic permeability.
Another way of increasing the power flow by increasing the ampere turns is not acceptable, since in order to save wire and power, one should strive to reduce the ampere turns.
Usually, calculations of electromagnets are made according to special schedules. To simplify the calculations, we will also use some conclusions from the graphs. Suppose it is necessary to determine the ampere-turns and power flux of a closed iron magnetic circuit, shown in Figure 4a and made of iron of the lowest quality.
Looking at the graph of iron magnetization, it is easy to see that the most advantageous magnetic induction is in the range from 10 000
up to
14,000
power lines per 1 cm2, which corresponds to from
2
to
7
ampere turns per 1 cm. To wind coils with the smallest number of turns and more economical in terms of power supply, this value must be taken for calculations (
10,000
power lines per 1 cm2 at 2 ampere turns per 1 cm length).
In this case, the calculation can be made as follows. So, with a magnetic circuit length Z=/1-)-/2
equal to
20 cm -f- 10 cm = 30 cm
,
2×30=60
ampere turns will be required.
For a two-pole magnet, this result should be doubled. Therefore, P=24.8 kg ^ 25 kg
. When determining the lifting force, it must be remembered that it depends not only on the length of the magnetic circuit, but also on the area of contact between the armature and the core. Therefore, the armature must fit exactly against the pole pieces, otherwise even the slightest air gaps will cause a strong reduction in lift.
Next, the electromagnet coil is calculated. In our example, the lifting force is 25 kg
provided by
60
ampere turns.
Let us consider by what means the product N-J—60
ampere turns can be obtained.
Obviously, this can be achieved either by using a large current with a small number of coil turns, for example 2 A and 30 turns, or by increasing the number of coil turns while reducing the current, for example 0.25 A and 240 turns. Thus, in order for an electromagnet to have a lifting force of 25 kg, both 30 turns and 240 turns can be wound on its core, but at the same time the value of the supply current can be changed. Of course, you can choose a different ratio.
Calculation of electromagnet windings
As a result of calculating the magnetic circuit, the required MMF of the winding is determined. The winding must be designed in such a way that, on the one hand, it provides the required MMF, and on the other, so that its maximum temperature does not exceed that permissible for the insulation class used.
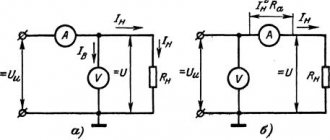
Depending on the connection method, voltage windings and current windings are distinguished. In the first case, the voltage applied to the winding is constant in its effective value, in the second, the resistance of the electromagnet winding is much less than the resistance of the rest of the circuit, which determines the constant value of the current.
Calculation of the DC electromagnet winding .
In Fig. Figure 4.8 shows the magnetic circuit and the electromagnet coil. Winding 1 of the coil is performed with an insulated wire, which is wound onto frame 2.
Reels can also be frameless. In this case, the winding turns are fastened with tape or sheet insulation or a potting compound.
To calculate the voltage winding, the voltage and MMF must be specified.
We find the cross-section of the winding wire based on the required MMF:
where is resistivity; - average coil length (Fig. 4.8); - winding resistance equal to .
From (4.13) it follows that, with a constant average coil length and a given MMF, it is determined by the product .
If, at a constant voltage and the average length of the turn, it is necessary to increase the MMF, then it is necessary to take a wire of a larger cross-section. In this case, the winding will have fewer turns. The current in the winding will increase, since its resistance will decrease due to a decrease in the number of turns and an increase in the cross-section of the wire.
The power released in the winding in the form of heat is determined as follows: .
The number of turns of the winding for a given coil cross-section is determined by the copper fill factor, where is the area occupied by the copper of the winding; – winding cross-section for copper. Number of turns. Then the power consumed by the winding is determined by the expression
To calculate the current winding, the initial parameters are MMF and circuit current.
The number of turns of the winding is found from the expression. The wire cross-section can be selected based on the recommended current density, equal to 2...4 A/mm 2 for long-term, 5...12 A/mm 2 for intermittent, 13...30 A/mm 2 for short-term operating modes.
These values can be increased by approximately 2 times if the service life of the winding and electromagnet does not exceed 500 hours. The window area occupied by an ordinary winding is determined by the number of turns and the diameter of the wire
Knowing , you can determine the average turn length, winding resistance and losses in it. After this, the winding heating can be assessed.
DC electromagnet calculation
Electromagnets have found wide application in apparatus engineering both as a device drive element (contactors, starters, relays, automatic machines, switches) and as a device that creates forces, for example, in clutches and brakes.
For a given flux, the drop in magnetic potential decreases with decreasing magnetic resistance. Since the resistance is inversely proportional to the magnetic permeability of the material, for a given flux the magnetic permeability should be as high as possible. This allows you to reduce the m.f. windings and power required to operate the electromagnet; The dimensions of the winding window and the entire electromagnet are reduced. Decrease in m.f.s. with other parameters unchanged, it reduces the winding temperature.
The second important parameter of the material is saturation induction. The force developed by an electromagnet is proportional to the square of the induction. Therefore, the greater the permissible induction, the greater the developed force for the same dimensions.
After the electromagnet winding is de-energized, there is a residual flux in the system, which is determined by the coercive force of the material and the conductivity of the working gap. Residual flow can cause the armature to stick. To avoid this phenomenon, the material is required to have a low coercivity.
Essential requirements are the low cost of the material and its manufacturability.
Along with the indicated properties, the magnetic characteristics of materials must be stable (not change from temperature, time, mechanical shocks).
As a result of calculating the magnetic circuit, the required magnetomotive force (MMF) of the winding is determined. The winding must be designed in such a way that, on the one hand, it provides the required MMF, and on the other hand, so that its maximum temperature does not exceed that permissible for the insulation class used.
Depending on the connection method, voltage windings and current windings are distinguished. In the first case, the voltage applied to the winding is constant in its effective value, in the second —
the resistance of the electromagnet winding is much less than the resistance of the rest of the circuit, which determines the constant value of the current.
Calculation of the DC electromagnet winding.
Figure 72 shows the magnetic circuit and the electromagnet coil. Winding 1
The coils are made with insulated wire, which is wound on frame
2.
The coils can also be frameless. In this case, the winding turns are fastened with tape or sheet insulation or a potting compound.
To calculate the voltage winding, the voltage U
and MDS.
The cross-section of the winding wire q
is found based on the required MMF:
where is resistivity;
– average coil length (Figure 72);
R
– winding resistance equal to
With a constant average coil length and a given MMF, it is determined by the product.
If, at a constant voltage and the average length of the turn, it is necessary to increase the MMF, then it is necessary to take a wire of a larger cross-section. In this case, the winding will have fewer turns. The current in the winding will increase, since its resistance will decrease due to a decrease in the number of turns and an increase in the cross-section of the wire.
Based on the found cross-section, using sizing tables, the nearest standard wire diameter is found.
Figure 72 – Calculation of the electromagnet winding
The power released in the winding in the form of heat is determined as follows:
The number of winding turns for a given coil cross-section is determined by the copper fill factor
where is the area occupied by the copper of the winding;
– winding cross-section for copper.
Then the power consumed by the winding is determined by the expression
To calculate the current winding, the initial parameters are MMF and circuit current. The number of turns of the winding is found from the expression. The wire cross-section can be selected based on the recommended current density, equal to 2...4 A/mm 2 for long-term, 5...12 A/mm 2 for intermittent, 13...30 A/mm 2 for short-term operating modes. These values can be increased by approximately 2 times if the service life of the winding and electromagnet does not exceed 500 hours. The window area occupied by an ordinary winding is determined by the number of turns and wire diameter d
Knowing , you can determine the average turn length, winding resistance and losses in it. After this, the winding heating can be assessed.
Source