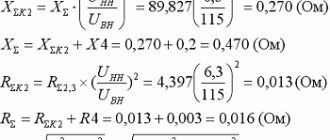Zone - spreading - current
Current spreading zone is a zone of the earth, beyond which the electric potential caused by ground fault currents can be conventionally assumed to be zero. [1]
In the current spreading zone (the space around the ground electrode within a radius of 20 m) there is a potential difference between any two points on the earth’s surface. [2]
Therefore, a person must leave the zone of spreading fault currents so that his steps are small, within 25 - 30 cm, then he will be subjected to the least voltage and will avoid electric shock. [3]
Therefore, a person must leave the zone of spreading fault currents so that his steps are small, within 25 - 30 cm, then he will be subjected to the least voltage and will avoid electric shock. [4]
The ground potentials in the current spreading zone are determined by the nature of the change in the electric field strength, which in turn is determined by the design of grounding devices and the parameters of the electrical structure of the earth. It is obvious that the earth's potential, all other things being equal, decreases with distance from the ground electrodes. [5]
In this case, it is recommended to get out of the zone of current spreading by jumping on one leg and placing the foot along the line of equal potential. [6]
If a person finds himself in the zone of current spreading and stands on the surface of the earth, which has different potentials in the places where the feet are located, then a step voltage will arise at the length of the step, corresponding to the difference in these potentials. An electric current will pass through the human body, the danger of which depends on its value. To prevent a person from getting under the Voltage of a step, you should not approach the place of damage at a distance of less than 4 - 5 m in enclosed spaces and 8 - 10 m in open substations. Only as a last resort to eliminate an accident or to provide first aid to the victim can you approach to the site of damage at a shorter distance - In this case, protective equipment should be used: boots, galoshes, rugs, wooden ladders, boards or other objects that do not conduct electric current well. [7]
Ground fault current spreading zone
Electrical injuries in most cases occur in single-phase (single-pole) modes when a person touches a live part of an electrical installation or non-current-carrying metal structures that accidentally become energized due to damage to the electrical insulation. Fire hazardous situations also, in most cases, arise in single-phase (single-pole) ground fault modes of current-carrying parts of an electrical installation due to operational damage to the insulation. In these modes, the values of currents in the circuits “current-carrying part - earth” or “live part - human body - earth” are determined by the parameters of the circuits connecting live parts to the ground not only through leakage resistance, as indicated in the previous article, but also through short circuit resistance ground or artificial grounding of live parts adopted in the electrical installation project.
Ground faults According to the Electrical Installation Rules (clause 1.7.10), a ground fault is an accidental connection of live parts of an electrical installation with structural parts not isolated from the ground, or with the ground directly. Near the location of the ground fault, a current spreading zone is formed - a space on the surface of which the electrical potentials are different from zero. The concept of this zone is one of the fundamental ones in the theory of electrical safety. Therefore, we will consider it in more detail, taking as an example an electric power transmission line (PTL). Suppose that for some reason there is a short circuit of phase wire C to a power line support (humidity, contamination of insulators, bird wings, etc.). The ground fault current flows along the circuit: phase C - power line support - earth - grounding resistance of the neutral R0 of the power line transformer - neutral 0 of the transformer (Fig. 1). A current spreading zone is formed near the power line support (its radius is considered to be 20 m). In this zone, current flows in the ground along radii in all directions from the support foundation. Therefore, in a simplified manner, the cross-section of the conductive layer of the earth can be taken as a hemisphere, the area of which is S = 2 px 2, where x is the distance to the support. That is, as you move away from the foundation of the support, the ground fault current flows as if through a conductor with a variable cross-section, increasing with distance from the fault point. The highest current density is observed near the fault point (here the smallest cross-section of the conductor is the ground). As you move away from the fault point, the cross-section of the conductor - the ground - increases and therefore the current density jzam = Izam / 2 px 2 gradually decreases to an infinitesimal value. Accordingly, the electric field strength in the current spreading zone E = r jzam (here r is the soil resistivity) changes from the maximum value to zero. That is, the potentials of the electric field in the current spreading zone change from the maximum value of j at the place of the ground fault to almost zero value at a distance of 20 m from the place of the fault. This pattern is typical for any type of ground fault (a fault to a power line support is taken only for clarity).
GROUND FAULT CURRENT SPREADING
GROUND FAULT CURRENT SPREADING
2.1 General information
Electric shock hazards are created by touch voltage or step voltage.
Touch voltage
. This is the voltage between two points in a current circuit that are simultaneously touched by a person.
Touch voltage is applied only to the human body and it is defined as the voltage drop in the human body according to (2.1)
where Ih is the current through a person, A; Rh – human resistance, Ohm.
With single-phase touch, the touch voltage depends on the voltage on the body relative to ground. With a two-phase touch, the touch voltage is equal to the operating voltage of the network.
When current flows along the leg-to-leg current path, a step voltage is created in the area near the ground electrode.
Step voltage
or step voltage is the voltage between two points located at the distance of a step on which a person simultaneously stands.
The current through a person also depends on the ground fault current. To calculate touch voltages and step voltages, let's consider the physical basis of their occurrence. Their occurrence is explained by the nature of the spreading of ground fault current.
2.2 Nature of earth fault current spreading
A ground fault can occur when a live part comes into contact with a grounded body, a breakdown of the insulation of high-voltage equipment, a broken wire falls, and a number of other reasons.
The grounded housing has a connection to the ground electrode of the grounding device. When there is a short circuit to the housing, the current passes through the ground electrode to the ground, Figure 2.1. The grounding current flows into the ground and a current spreading field is created around the ground electrode. The parameters of the spreading field depend on different conditions. These include the shape and size of the ground electrode, soil composition, soil moisture, time of year, and so on.
To determine the parameters, certain assumptions and simplifications are made in order to obtain an overall picture of current flow.
A single hemispherical ground electrode is used as a ground electrode. The soil is considered homogeneous with resistivity r. The spreading current lines are directed along radii from the center of the hemispherical ground electrode and are perpendicular to its surface.
Figure 2.1 — Ground fault current spreading
If the soil is homogeneous, then the fault current is evenly distributed over its surface, with a certain current density d.
Concentric spheres are formed around the ground electrode. The points of each sphere correspond to the same current density and intensity. Such a surface is called equipotential
surface, Figure 2.1.
The current density along the soil surface decreases with distance from the ground electrode, as can be seen from formula (2.2)
where is the distance from the center of the ground electrode to any point “A” of the soil surface, m; IЗ - circuit current, A.
The farther from the ground electrode, the lower the current density. At great distances, the current density is practically zero.
Each point of the ground, having a certain current density, has an electric potential jA = UA.
To determine the potential at point A, we select an elementary layer of soil with a thickness at a distance from the ground electrode; the potential difference or voltage drop in this layer is equal to (2.3)
where E is the electric field strength.
The electric current intensity at point A will be determined from (2.4)
The potential of point jA=UA is equal to the total voltage drop from point A to an infinitely distant point with zero potential (2.5). All points at which the current density is zero have zero potential. Substituting formulas (2.2) and (2.4) into (2.5), we obtain expression (2.6) for calculating the potential of point A.
To determine the general dependence of the change in the potentials of the fault current spreading region, it is taken into account that (2.6) will take the form (2.7)
This is a hyperbolic dependence of the potential distribution in the spreading zone of a spherical ground electrode, Figure 2.2. As the point in question moves away from the ground electrode, the potential decreases and practically reaches zero. If you place the point under study on the surface of the ground electrode with a radius , the potential will be greatest, equal to (2.8)
Spreading of current in the ground during a ground fault.
Answer: Current flows into the ground only through a conductor in direct contact with the ground. Such contact may be accidental or intentional.
In the latter case, the conductor or group of interconnected conductors in contact with the ground is called a ground electrode. In addition, a single conductor in contact with the ground is also called a single grounding electrode, or a grounding electrode, or simply an electrode, and a grounding electrode consisting of several parallel-connected electrodes is also called a group or complex grounding electrode.
The reasons for the flow of current into the ground are: short circuit of the current-carrying part to the grounded body of electrical equipment, falling of the wire to the ground, use of the earth as a wire, etc. In all these cases, there is a sharp decrease in the potential (i.e., voltage relative to the ground) of the grounded current-carrying line parts to a value equal to the product of the current flowing into the ground I
h, A, to the resistance that this current encounters on its path, i.e.
grounding resistance to current spreading, Rz,
Ohm:
Фз=Iз*Rз.
This phenomenon, which is very favorable in terms of safety, is used as a measure of protection against electric shock when voltage accidentally appears on metal non-current-carrying parts, which are grounded for this purpose. However, along with a decrease in the potential of the grounded current-carrying part, when current flows into the ground, negative phenomena also arise, namely the appearance of potentials on the ground electrode and metal parts in contact with it, as well as on the soil surface around the place where the current flows into the ground. The resulting potential differences at individual points in the current circuit, including points on the earth's surface, can reach large values that pose a danger to humans.
Touch voltage with single and group grounding.
Answer:
Touch voltage Upr is the potential difference between two points of the current-carrying circuit, in cat. person included.
Upr=Ih*Rh (where Ih is the current passing along the hand-leg path, Rh is the resistance of the human body). In the field of protective grounding, grounding, etc. one of these points has the ground potential φз, V, and the other has the potential of the base in the place where the person stands, φos, V.
In this case, the touch voltage will be: Upr= φз- φос= φз*α1, where α1 is a coefficient called the touch coefficient, which takes into account the shape of the potential curve.
Touch voltage with a single grounding electrode: Let us have equipment, for example, electric motors, the housings of which are grounded using a single grounding electrode (Fig. 14.4). When one of these motors is shorted to the housing (lightning arrow) on the grounding electrode and on all metal connected to it parts, including on engine housings, the potential Upr will appear.
The surface of the earth around the ground electrode will also have a potential that varies along a curve depending on the shape and size of the ground electrode. The touch voltage for a person touching the grounded engine housing and standing on the ground (case 1) is characterized by the segment AB and the shape of the potential curve and the distance (x) between the person and the ground electrode: the farther the person is from the ground electrode, the greater Upr. Safe cases: At the lowest value of x ,
those. when a person stands directly on the ground electrode (case 3).
Touch voltage with a group grounding electrode: The spreading fields of the currents of the electrodes of the group grounding electrode are superimposed on one another, all surface points in the area between the electrodes have potentials different from 0. Therefore, anywhere in this area Upr
Current spreading in the ground
2015-05-26 8490
A ground fault can occur due to contact between live parts and a grounded frame when the electrical insulation of the equipment is damaged, a broken wire falls to the ground, etc. In these cases, the current flows into the ground through an electrode that is in contact with the ground. A metal conductor (electrode) immersed in the ground is called a ground electrode.
The current, flowing from the ground electrode into the ground, is distributed over a significant volume of it. The space around the ground electrode, where the potentials are not equal to zero, is called the current spreading field. If a person is in the field of current spreading, then the current passes through his legs.
The voltage between two points of an electrical current circuit, located one step apart from each other, on which a person is simultaneously standing, is called step voltage or step voltage.
The law of potential distribution in the electric field of the ground electrode is described by a complex relationship determined by the size, shape of the ground electrode and the electrical properties of the soil.
To identify the law of distribution of ground potentials in the current spreading field, we make the following assumption: current I
W flows into the ground through a single hemispherical ground electrode of radius
r
immersed in homogeneous isotropic soil with electrical resistivity r (Fig. 1).
The spreading current lines are directed along radii from the ground electrode as from the center, and the sections of the earth as a conductor are hemispheres with radii r
Rice. 2 Potential distribution curves of a hemispherical ground electrode
Ground electrode potential with radius r
or grounding voltage relative to ground:
(6)
The ground electrode has the highest potential. Points lying on the ground surface have a lower potential the further they are from the ground electrode. At the limit, the potential of remote ground points tends to zero. The reason for this distribution of potentials lies in the peculiar shape of the conductor (earth), the cross-section of which increases in proportion to the second power of the radius of the hemisphere (Fig. 3).
The current flowing from the ground electrode spreads over the ground, which resists the flow of current. The resistance to current spreading of the ground electrode is defined as the total resistance of the soil from the ground electrode to the point with zero potential. For a hemispherical ground electrode located in a homogeneous isotropic soil, the spreading resistance R
RAS has the form:
(7)
The greatest resistance to current spreading is provided by the layers of earth (soil) lying near the ground electrode, since the current flows here through a small cross-section. The greatest voltage drops occur at these points.
Rice. 3 Simplified model of earth conductor
As you move away from the ground electrode, the cross-section of the conductor (earth) increases and the resistance to current flow decreases, and therefore the voltage drop decreases. At a distance of 10¸20 m from the ground electrode, the cross-section of the conductor (earth) becomes so large that the earth offers virtually no resistance to the passing current. Thus, the potential of ground points located at a distance of 10¸20 m from a single hemispherical ground electrode is practically zero.
Step voltage is defined as the potential difference between points, for example A and B (see Fig. 4).
Since point A is removed from the ground electrode at a distance
r
, then its potential, based on (5) with a hemispherical ground electrode, is obtained in the form:
Point B is located at a distance r+a from the ground electrode,
i.e. point B is distant from point A by the amount of person’s step
a.
Point B potential:
Rice. 4 The emergence of stepper
The step voltage is greatest near the ground electrode. As you move away from the ground electrode, the step voltage decreases. If a person’s feet are at the same distance from the ground electrode, i.e. on a line of equal potential (equipotential), then the step voltage is zero. Let the distance from the ground electrode to the equipotential at which a person is located be equal to r
, then the step voltage is zero.
The value of the step voltage depends on the step size. Reducing it leads to a decrease in step voltage. The step voltage depends on the grounding voltage:
where is the step voltage coefficient, taking into account the shape of the potential curve.
The step voltage coefficient bШ depends on the shape and configuration of the ground electrode and the position relative to the ground electrode of the point at which it is determined. The closer to the ground electrode, the greater bSh and, therefore, the greater the step voltage. A person located outside the current spreading field (at a distance of 10–20 m from the ground electrode) is not affected by the step voltage, since bSh = 0. As can be seen from the expression for determining the step coefficient, its value is less than unity. Thus, the step voltage is part of the ground electrode voltage. The resulting expression for determining bSh is valid only for a hemispherical ground electrode.