In foreign terminology, the abbreviation RMS (rms) is used - root mean square. In mathematics, for a set of numbers x1, x2, ..., xn of number n, the root mean square value (rms) is determined by the expression:
For example, for the numbers 2,3 and 6, the root mean square value is the square root of (2²+3²+6²)/3. √(49/3) = 4.04
The root mean square of two or more numbers is the square root of the arithmetic mean of the squares of those numbers.
For any continuous function in the interval T
1 -
T
2 root mean square value can be calculated using the formula:
The root mean square value is used in calculations where there is a proportional dependence not of the variable values themselves, but of their squares.
RMS voltage and current
As an example, we can consider the quadratic dependence of the power or work of an electric current on the values of current or voltage.
P = I²R; A = I²Rt; P = U²/R; A = U²t/R
The magnitude of a direct voltage or current is its root mean square value. The rms value of the alternating current is equal to the value of the direct current, the action of which will produce the same work in a resistive (resistive) load during the period. The determining factor here is the average (arithmetic mean) value of power P
avg or work
A
avg, proportional to the square of the current value. Also, the root-mean-square value of the alternating voltage over a period is equivalent in its effect on the active load to the same value of the direct voltage.
P=UI=P
avg
= U
rms
I
rms
The rms value of alternating voltage or current is often called effective or effective.
The magnitude of alternating voltage or current, in most cases, is expressed by its root-mean-square value and measured with electromagnetic-type devices or special root-mean-square meters - True RMS.
Note: Electromagnetic instruments are used to measure alternating current and voltage in industrial installations. The force created by the measuring coil in an electromagnetic device is proportional to the square of the current, and therefore does not change in direction. The angle of deflection of the needle will be determined by a certain average force F, which will be proportional to the root-mean-square value of the current.
Types of differential currents
The whole variety of differential currents that can arise in the main circuit of a household differential current device, in the GOST IEC 61008-1-2020 [3] and GOST IEC 61009-1-2020 [4] standards, is reduced to the following two types: sinusoidal differential current and pulsating direct differential current .
Kharechko Yu.V. in his book [2], in my opinion, he described in the simplest possible terms the features of these 2 types of differential current. Here are the main quotes:
“Sinusoidal differential current occurs in cases where rectifiers, dimmers, adjustable electric drives and similar devices that significantly change the shape of the sinusoidal current are not used in the alternating current electrical circuits that are connected to the differential current device. The leakage current and ground fault current in such electrical circuits have a shape close to a sinusoid. The differential current has the same sinusoidal shape (Fig. 2).
Rice. 2. Sinusoidal current with a frequency of 50 Hz (based on Figure 2 from [2] by Yu.V. Kharechko)
When rectifiers, dimmers, adjustable electric drives and similar devices are used in electrical installations of buildings, the shape of the sinusoidal current in electrical circuits can change significantly.
If a diode is used in some electrical receiver as a discrete regulator of its power consumption, in the event of damage to the main insulation of the current-carrying part connected after the diode, a ground fault current may occur, which will flow only for half a period (180° or 10 ms) . Such electric current is called pulsating direct current in the GOST IEC 61008-1-2020 and GOST IEC 61009-1-2020 standards. The flow of pulsating direct current in the main circuit of a differential current device significantly changes its characteristics compared to sinusoidal current.
In electrical installations of residential buildings, a large number of electrical receivers with built-in rectifiers are used. All are characterized by small DC leakage currents which can create a total (background) DC leakage current flowing through the main circuit of the residual current device. The flow of even a small direct current through the primary winding of a differential transformer UDT significantly changes (worsens) its characteristics. Therefore, the GOST IEC 61008-1-2020 and GOST IEC 61009-1-2020 standards take into account the possibility of a small direct current flowing through the main circuit of the differential current device.
Pulsating direct current is defined in international and national standards as wave-like pulses of electric current with a duration (in angular measure) of at least 150° per pulsation period, following periodically with a nominal frequency and separated by time intervals during which the electric current takes on a zero value or a value not exceeding 0.006 A DC.
Pulsating direct current is also characterized by the current delay angle, which is understood as the period of time in angular value during which the phase control device delays the flow of electric current in the electrical circuit. In Fig. 3 and 4 show pulsating direct current at current delay angles α equal to 0°, 90° and 135°.
Rice. 3. Pulsating direct current with a frequency of 50 Hz without a direct current component (based on Figure 3 from [2] by Yu.V. Kharechko)
Rice. 4. Pulsating direct current with a frequency of 50 Hz with a direct current component up to 0.006 A inclusive ((based on Figure 4 from [2] by Yu.V. Kharechko)
The appearance of pulsating direct current in the main circuit of the differential current device significantly changes the characteristics of the UDT. AC residual current devices, which are designed to operate only with sinusoidal current, cannot function correctly when pulsating direct current appears. Therefore, in some countries their use in electrical installations of buildings is prohibited or significantly limited. Type AC residual current devices are being replaced by more modern type A UDTs, which are designed for use with both sinusoidal and pulsating direct current.
In 2021, GOST IEC 62423-2013 was introduced, which applies to type F and type B UDTs for domestic use. Type F UDTs are designed to protect electrical circuits to which frequency converters are connected. They operate in the same way as UDT type A, and additionally:
- with complex differential currents;
- with a pulsating dc differential current superimposed on a smoothed dc current of 0.01 A.
Type B residual current devices operate in the same way as type F UDTs, and additionally:
- with sinusoidal alternating differential currents with a frequency of up to 1000 Hz inclusive;
- with a pulsating direct differential current that appears in two or more phases;
- with smoothed constant differential currents.
Thus, the most modern type B UDTs operate correctly in AC electrical circuits when ground fault currents of various forms flow through them, ranging from a sinusoidal current with a frequency of 50 Hz and ending with direct current. »
AC average value
Publication date: March 26, 2015.
Category: Articles. The average value of the sinusoidal variable over the period is zero. Therefore, when they talk about the average value of a sinusoidal value, they mean the average value over half a period. Figure 1 shows the curve of alternating current changes over half a cycle.
Figure 1. Average value of sinusoidal current
Let's construct a rectangle with base T/2 and area equal to the area enclosed between the curve and the horizontal axis. The height of the rectangle will represent the average current value over half a cycle.
Higher mathematics gives the following relationship between the average and amplitude values of an alternating sinusoidal current:
The same relationship exists between the average and amplitude values of voltage and electromotive force (EMF). The average value of voltage and emf is:
The ratio of the effective value of a variable to its average value is called the curve shape coefficient and is denoted by the letter kf.
For sinusoidal quantities, the curve shape factor is:
The ratio of the amplitude value of a variable to its effective value is called the amplitude coefficient and is denoted ka.
For sinusoidal quantities, the crest factor
Source: Kuznetsov M.I., “Fundamentals of Electrical Engineering” - 9th edition, revised - Moscow: Higher School, 1964 - 560 p.
Source
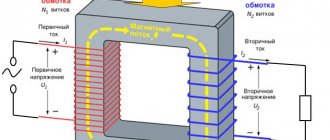
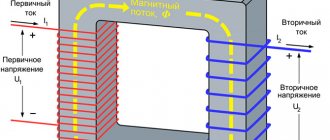
Determination of transformer no-load current
The current generated in the primary winding of a transformer during no-load operation at rated sinusoidal voltage and rated frequency is called no-load current.
When calculating the no-load current of a transformer, its active and reactive components are determined separately.
The active component of the no-load current is caused by the presence of no-load losses.
Active current component, A:
, (7.19)
where Рх – no-load losses, W;
Uph – phase voltage of the primary winding, V.
Usually, it is not the absolute value of the no-load current and its components that is determined, but their relative value in relation to the rated current of the transformer i
oa,
i
op,
i
o, expressing them as a percentage of the rated current.
Then the active component, %:
, (7.20)
where S is the power of the transformer, kVA;
Рх – no-load losses, W.
The calculation of the reactive component of the no-load current is complicated by the presence of non-magnetic gaps in the magnetic circuit of the transformer. In this calculation, the magnetic system of the transformer is divided into four sections - rods, yokes, with the exception of the corners of the magnetic system, corners and gaps. For each of these sections, the required magnetizing power is calculated, which is then summed over the entire magnetic system. Just like losses, the reactive component of the no-load current depends on the basic magnetic properties of the steel of the magnetic system and a number of design and technological factors that have a significantly greater influence on this component than on losses [5].
And so for a flat three-phase laminated magnetic system with mutual arrangement of rods and yokes, assembled from plates of cold-rolled anisotropic steel , the total magnetizing power can be calculated by the formula, VA:
, (7.21)
where Gс, Gя/ and Gу are the masses of steel rods, individual parts of yokes and corners, respectively, kg;
qс and qя – specific magnetizing powers for steel rods and yokes, (determined according to Table 7.5), VA/kg;
qз – specific magnetizing power for gaps, determined according to Table 7.5, by induction for straight and oblique joints, similar to рз when calculating no-load losses, VA/m2;
Pz – gap area, determined in the same way as when calculating no-load losses, m2;
kt.r – coefficient taking into account the effect of cutting the coil strip on the plates: for annealed steel kt.r=1.18, for unannealed steel kt.r=1.49;
kt.z is a coefficient that takes into account the effect of cutting burrs: for annealed plates kt.z=1.0, for unannealed plates kt.r=1.01;
kt.y is a coefficient that takes into account the number of angles with oblique and straight joints of the magnetic system plates according to Table 7.6;
kt.pl - coefficient taking into account the width of the plates in the corners of the magnetic system according to Table 7.7;
kt.i – coefficient taking into account the cross-sectional shape of the yoke, kt.i=1.0 for a yoke with a multi-stage section and kt.i=1.07 for a yoke of rectangular cross-section (with the ratio of the number of legs of the rod and yoke equal to three, kt.i= 1.04; with a ratio of six kt.i=1.06);
kt.p is a coefficient that takes into account the pressing of the magnetic system according to Table 7.4;
kt.sh - coefficient taking into account the over-mixing of the upper yoke, equal to 1.01 with a transformer power of up to 250 kVA; 1.02 at powers of 400-630 kVA.
Table 7.5 - Total specific magnetizing power in steel q [V∙A/kg] and in the area of the laminated joint q3 for cold-rolled steel grades 3404 and 3405 with a thickness of 0.35 and 0.30 mm at various inductions and f = 50 Hz
| V, T | Steel grade and thickness | qз, V∙A/m2 | ||||
| 3404, 0.35 mm | 3404, 0.30 mm | 3405, 0.35 mm | 3405, 0.30 mm | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0,20 | 0,040 | 0,040 | 0,039 | 0,038 | ||
| 0,40 | 0,120 | 0,117 | 0,117 | 0,115 | ||
| 0,60 | 0,234 | 0,230 | 0,227 | 0,223 | ||
| 0,8 | 0,375 | 0,371 | 0,366 | 0,362 | ||
| 1,00 | 0,548 | 0,540 | 0,533 | 0,525 | ||
| 1,20 | 0,752 | 0,742 | 0,732 | 0,722 | ||
| 1,22 | 0,782 | 0,768 | 0,758 | 0,748 | ||
| 1,24 | 0,811 | 0,793 | 0,783 | 0,773 | ||
| 1,26 | 0,841 | 0,819 | 0,809 | 0,799 | ||
| 1,28 | 0,870 | 0,844 | 0,834 | 0,824 | ||
| 1,30 | 0,900 | 0,870 | 0,860 | 0,850 | ||
| 1,32 | 0,932 | 0,904 | 0,892 | 0,880 | ||
| 1,34 | 0,964 | 0,938 | 0,924 | 0,910 | ||
| 1,36 | 0,996 | 0,972 | 0,956 | 0,940 | ||
| Continued from Table 7.5 | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1,38 | 1,028 | 1,006 | 0,988 | 0,970 | ||
| 1,40 | 1,060 | 1,040 | 1,020 | 1,000 | ||
| 1,42 | 1,114 | 1,089 | 1,065 | 1,041 | ||
| 1,44 | 1,168 | 1,139 | 1,110 | 1,082 | ||
| 1,46 | 1,222 | 1,188 | 1,156 | 1,123 | ||
| 1,48 | 1,276 | 1,238 | 1,210 | 1,161 | ||
| 1,50 | 1,330 | 1,289 | 1,246 | 1,205 | ||
| 1,52 | 1,408 | 1,360 | 1,311 | 1,263 | ||
| 1,54 | 1,486 | 1,431 | 1,376 | 1,321 | ||
| 1,56 | 1,575 | 1,511 | 1,447 | 1,383 | ||
| 1,58 | 1,675 | 1,600 | 1,524 | 1,449 | ||
| 1,60 | 1,775 | 1,688 | 1,602 | 1,526 | ||
| 1,62 | 1,958 | 1,850 | 1,748 | 1,645 | ||
| 1,64 | 2,131 | 2,012 | 1,894 | 1,775 | ||
| 1,66 | 2,556 | 2,289 | 2,123 | 1,956 | ||
| 1,68 | 3,028 | 2,681 | 2,435 | 2,188 | ||
| 1,70 | 3,400 | 3,073 | 2,747 | 2,420 | ||
| 1,72 | 4,480 | 4,013 | 3,547 | 3,080 | ||
| 1,74 | 5,560 | 4,953 | 4,347 | 3,740 | ||
| 1,76 | 7,180 | 6,364 | 5,551 | 4,736 | ||
| 1,78 | 9,340 | 8,247 | 7,161 | 6,068 | ||
| 1,80 | 11,500 | 10,130 | 8,770 | 7,400 | ||
| 1,82 | 20,240 | 17,670 | 15,110 | 12,540 | ||
| 1,84 | 28,980 | 25,210 | 21,450 | 17,680 | ||
| 1,86 | 37,720 | 32,750 | 27,790 | 22,820 | ||
| 1,88 | 46,460 | 40,290 | 34,130 | 27,960 | ||
| 1,90 | 55,200 | 47,830 | 40,740 | 33,100 | ||
| 1,95 | 89,600 | 82,900 | 76,900 | 70,800 |
Note: when blending into one plate, multiply the q3 data by 0.82 for steel grade 3404 and by 0.78 for steel grade 3405.
Table 7.6 - Values of the coefficient kt.u., for a different number of angles with oblique and straight joints of plates of a flat laminated magnetic system for steel grades 3404 and 3405 with a thickness of 0.35 and 0.30 mm at f = 50 Hz
| Number of corners with joints | Induction V, T | |||||
| oblique | straight | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 |
| — | 26,0 | 27,95 | 27,95 | 26,0 | 22,10 | |
| 5* | 1* | 32,25 | 34,83 | 35,20 | 33,25 | 27,85 |
| 38,5 | 41,7 | 42,45 | 40,5 | 33,66 | ||
| — | 58,5 | 64,7 | 65,6 | 64,7 | 52,0 |
Table 7.7 - Values of the coefficient kt.pl, taking into account the increase in magnetizing power in the corners of the magnetic system depending on the width of the plate of the second package a2 for cold-rolled steel
| V, T | Width of the plate of the second package a2, m | |||||||
| 0,05 | 0,10 | 0,20 | 0,30 | 0,40 | 0,50 | 0,60 | 0,70 | |
| 0,8-1,00 | 1,30 | 1,25 | 1,20 | 1,17 | 1,15 | 1,14 | 1,13 | 1,12 |
| 1.10 and 1.90 | 1,40 | 1,27 | 1,21 | 1,18 | 1,16 | 1,15 | 1,14 | 1,13 |
| 1.20 and 1.80 | 1,50 | 1,30 | 1,22 | 1,19 | 1,17 | 1,16 | 1,15 | 1,14 |
| 1.30 and 1.70 | 1,70 | 1,38 | 1,25 | 1,21 | 1,18 | 1,17 | 1,16 | 1,15 |
| 1.40 and 1.60 | 2,00 | 1,50 | 1,35 | 1,25 | 1,20 | 1,19 | 1,18 | 1,16 |
| 1,50 | 3,00 | 2,0 | 1,50 | 1,35 | 1,30 | 1,25 | 1,20 | 1,18 |
Absolute phase value of the reactive component of the no-load current, A:
(7.22)
The relative value of the no-load current as a percentage of the rated current of the transformer (similar to the active component i
oa) , %:
(7.23)
Total no-load current, A:
Ix = (7.24)
and as a percentage of rated current:
io =
(7.25)
The resulting value of the no-load current is i0
should be checked with the no-load current according to the instructions for calculating the transformer - I0, i.e. this deviation should not exceed 70%.
Previous9Next
Conflicts in family life. How can I change this? It is rare that a marriage and relationship exists without conflict and tension. Everyone goes through this...
What will happen to the Earth if its axis shifts by 6666 km? What will happen to the Earth? - I asked myself...
WHAT IS CONFIDENT BEHAVIOR IN INTERPERSONAL RELATIONSHIPS? Historically, there are three main patterns of differences that exist between...
What makes your dreams come true? One hundred percent, unshakable confidence in your...
Didn't find what you were looking for? Use Google search on the site: