Calculation of a three-winding transformer
Neglecting the no-load current, we can write the equation for the currents of a three-winding transformer:
I1= — (I2'+ I3'),
that is, the primary current is equal to the geometric sum of the reduced secondary currents.
In this case, we will get two transformation coefficients k12 and k13 between the first and second and between the first and. third windings of the transformer. As a general rule:
k12=E1/E2=w1/w2
k13=E1/E3=w1/w3
Using the known two transformation ratios, it is possible to determine the third k23 between the second and third windings:
k23=E2/E3=w2/w3=k13/k12
The rated power of a three-winding transformer is the power of its most powerful winding, which is always the HV winding. Manufacturing a three-winding transformer in the case where the power of one of its secondary windings is small is uneconomical. Therefore, the power of the HV, MV, LV windings of a three-winding transformer as a percentage of its rated power is usually:
· 100/100/100;
· 100/100/66,7;
· 100/66,7/100;
· 100/66,7/66,7.
Three-winding transformers are usually built for high powers: 5600-31500 kW (three-phase) and 5000-40,000 kW (single-phase) with a voltage of the HV windings 110 - 121 kV; MV 34.5 - 38.5 kV and LV 3.15 - 15.75 kV.
In some cases, three-winding transformers with two primary and one secondary winding are used. Such transformers are used at large power plants when there is a need to operate two or three generators on a common power line through one powerful step-up transformer. Sometimes transformers have two primary windings with different voltage ratings.
Selection of three-winding transformers and transformers with a split low voltage (LV) winding.
For sharply variable and quiet loads in networks with a voltage of 6-10 kV, power transformers with split windings are used.
Oscillogram of a primary six-phase valve converter when connecting the network winding of an anode transformer to a star / \ _i_ ——————- _| —— *.
In furnace transformers, the secondary voltage windings are connected in a triangle, so the current does not contain harmonics that are multiples of three.
As a result, harmonics of the order v = 6fe + 1 are present in the primary windings of the transformers of both units, but only harmonics of the order v = 12/s + 1 enter the supply network, and the remaining current harmonics circulate between the primary windings of the transformers.
This EMF causes a pulsating field in the excitation winding, which is decomposed into two components: a field rotating in the direction of rotation of the rotor and inducing an EMF of triple frequency in the stator, and a field rotating in the direction opposite to the direction of rotation of the rotor, and inducing an EMF in the stator with a rotation frequency the main negative sequence field, partially compensating it.
These installations are powered by alternating current of industrial frequency from special transformers with a voltage of 6-10 kV on the primary winding, and up to 110 kV on the secondary winding.
3) the excess of the temperature of the hottest point of the winding over the average temperature of the winding was equal to 130 °C;
6) during transient processes during the day, the highest temperature of the upper layers of oil did not exceed 95 °C and the hottest point of the winding metal did not exceed 140 °C.
The execution of one winding with an on-load tap-changer is indicated by the additional letter H.
A transformer with a split LV winding is designated by the letter P after the number of phases, for example TRDN.
The rated power and voltage class are indicated as a fraction, the numerator of which is the rated power in kilovolt-amperes, and the denominator is the voltage class of the HV winding in kilovolts.
Thermal capacity of transformers with copper windings
cm = 132G0 + 108G(,P + 545GM + 133GMar; transformers with aluminum windings
Selection of three-winding transformers and transformers with split low voltage (LV) windings
In industrial power supply systems, three-winding transformers are often installed to provide power to consumers at different voltages or transformers with a split LV winding.
Transformers with split LV winding are widely used in power supply systems of ferrous and non-ferrous metallurgy enterprises, where sharply variable nonlinear loads occur (for example, powerful valve converters of rolling mills) (Fig.
18) to reduce their impact on the supply network and improve technical and economic indicators, it is desirable to perform with a large number of phases. In this case, installing one transformer with split LV windings is preferable to installing two two-winding transformers.
In this case, the LV windings must be made with connections of different groups.
Technical data of three-winding transformers and transformers with a split LV winding are given in [17, 19].
One of the main characteristics of transformers with split windings is the splitting coefficient /ср, which characterizes the electromagnetic coupling between the LV windings and is determined as follows:
19, i), then their resistance on the three-beam equivalent circuit is equal to zero, all the resistance of the transformer turns out to be concentrated in the branch corresponding to the primary winding.
This means that when, for example, current 12 changes, not only the voltage of this winding U2 changes, but also the voltage Uз, since current 12 causes a voltage drop by zt, which leads to a change in voltage U3.
Schematic diagrams of windings and equivalent circuits of transformers with split low voltage (LV) windings: a, 6 - schematic diagrams; c, d - equivalent circuits
It is obvious that for a GPP transformer, to the LV windings of which a dissimilar load is connected, the equivalent circuit should be similar to that shown in Fig.
19, d, since in this case the loads of the windings have practically no effect on each other and the voltage levels on each winding depend only on their own load.
For a valve converter, on the contrary, from the point of view of limiting short-circuit currents and the rate of increase of current di/dt when switching valves, it is desirable that the transformer resistance be concentrated in the branch corresponding to the higher voltage winding.
But when the converter operates in normal modes, this will not happen, since the LV windings have different connection patterns (for bridge circuits - star-delta, and for zero - two reverse stars) and the current switching times in them do not coincide.
The method for calculating the resistance of equivalent circuits of three-winding transformers and transformers with a split LV winding is based on the use of the initial data in Table.
At the stage of preliminary calculations for existing designs of three-phase transformers with 1/„ohm = 10-=-220 kV with a split LV winding, made according to the diagram in Fig.
Due to the fact that in the catalog data the losses in the metal of the windings of three-winding transformers are given for loading 100% of each winding, the calculated losses do not correspond to the actual ones, with an error towards overestimation.
nn, (6-26) where APX is the power loss of the XX transformer; AP0|U - power of cooling devices; APk,BH - power losses in the metal of the HV winding at 100% load; /se,vn - load factor of the HV winding; APk,сн - power losses in the metal of the MV winding at 100% load; /с3_сн — load factor of the CH winding; AP^nn - power loss in the metal of the LV winding at 100% load; &зНн~кое4ь loading factor of the LV winding.
Calculation of the resistance of equivalent circuits of three-winding transformers and transformers with a split LV winding
Three-phase transformer with a low-wf winding “nom, t> kVA; ^kVN-NN.
torus with a winding of lower GL ^nom, t> kV-A; , — _ ,.
DRC vn-nn - power losses in the HV and LV windings; DRK_vn-sn - power losses in the HV and MV windings; DRkSN_nn - power losses in the MV and LV windings.
To determine the losses when loading each winding at the rated power of the transformer, we compose the equations
The highest upper excitation limit of a synchronous motor is determined by the permissible temperature of the rotor winding with a time delay sufficient to force excitation during short-term voltage drops.
The excitation current in this case is the rectified operating current of the stator winding.
The three-phase bridge rectifier in this case operates in short-circuit mode, due to which the same currents flow through the stator winding as when it is connected in a star.
When contact K is open, the rotor winding is powered by rectified stator current and the motor operates in synchronous mode.
Since there is a large inductive resistance of the stator winding at the rectifier input, and the active resistance of the rotor winding is relatively small (no more than 0.1 rel.
Thus, the series connection of the rotor winding through a rectifier device has virtually no effect on the duration of current flow in the phases of the stator winding.
When overloaded or out of synchronism, the EMF in the rotor winding sharply increases, under the influence of which the thyristor Vs opens and simultaneously shunts the rectifier and the rotor winding, i.e.
The excitation current and emf, reduced to the stator winding, are determined as follows: /, = /,?
52) where k = ktke/k3 is the synchronization coefficient; k3 is the equivalence coefficient according to the MMF of the rotor winding (k3 = 1.23 when the rotor is powered through two rings; k3 - 1.41 - the same, but through three rings).
— active resistance of the stator winding; xj is the leakage reactance of the stator winding; r^ is the active resistance of the magnetizing branch (equivalent to losses in steel); xc — mutual inductance reactance; xe, r, are the reactive and active equivalent resistances of the rectifier and rotor winding, respectively; a = Lhm
In power systems with isolated neutral voltages up to 1000 V, transformers associated with systems with voltages above 1000 V are protected from dangerous damage between the high and low voltage windings of the transformer by a breakdown fuse, which is installed in the neutral and phase on the low voltage side of the transformer.
1) preventing dangerous consequences in the event of an insulation breakdown between the high and low voltage windings of the transformer;
zКз,з, where ДРк',ь АР к, а, ДРк,з - reduced active power losses in the windings of high (1), medium (2) and low (3) voltages; K3ii, K3,2, K3,z - load factors of these windings.
The resistance of the rotor winding reduced to the stator is determined by the formula g g = where Ui is the linear voltage of the stator; [72k is the linear voltage on the rotor rings.
Additional averaged active power losses in the windings of a synchronous machine [16]
/^lv - additional active power losses in the statorv = 3rd winding; 3?
I*R'i>v ~ additional active power losses v = 3 in the rotor winding; Rlv is the active resistance of the stator winding of a synchronous machine for the v-th harmonic; ^2,jV is the equivalent active rotor resistance for the positive sequence current of the v-th harmonic.
2) Additional losses of active power in the windings of an asynchronous motor, caused by currents of higher harmonics, are determined by the formula
When using average machine parameters, additional active power losses in the stator and rotor windings from higher harmonic currents can be calculated approximately.
Losses in the stator windings (ARns1) are determined as a part of the nominal losses in copper according to the formula
53) where /”start = l/zK - multiplicity of starting current at rated voltage; AP]HOM - losses in the stator winding at rated current.
Additional active power losses in the rotor windings of an asynchronous motor
Total losses in the windings of an asynchronous motor
The main part of the additional active power losses from higher harmonics in synchronous machines falls on the damper winding and stator winding.
In high-voltage asynchronous motors, additional active power losses from higher harmonics in the stator and rotor windings are comparable in value.
Since the permissible duration of a one-and-a-half-time overload for generators with indirect cooling of the stator and rotor windings is 2 minutes, then t„o„,n = 120 =1 = ~.
This is explained by higher nominal current densities in their windings and uneven heating of the windings during overloads due to heating of the cooling medium in the channels.
The voltage boosting capacity is considered to be the ratio of the highest steady-state voltage (ceiling) t/B,n,y of the exciter (connected to the excitation winding of the generator) to the rated excitation voltage L'BHOM, and the current boosting capacity is understood as the ratio of the limit (the highest permissible for heating the winding rotor) of the excitation current /„_„, created by the exciter in the boost mode, to the rated excitation current /v>nom.
T - time from the moment of shunting by the shunt rheostat; /-current in the shunt winding; I/;, - armature voltage; I—current curve; 2 - voltage curve
Oscillogram of the process of forcing the excitation of turbogenerators at 15% overload: a - TV-60-2 with exciter VT-170-3000; b -TA2-100-2 with pathogen VT-300-3000; G„ is the moment of shunting the shunt rheostat; [/v - ceiling armature voltage; / - boost shunt winding current for turbogenerators operating with 10 - 20% overload are given in table.
When calculating these values, the excitation voltage at the maximum possible overload is taken to be the voltage at a rotor winding temperature of 100 °C.
Winding Stator voltage, kV Cooling gas temperature, °C up to 30 31-35 36-40 41-45 46-50 51-55
Winding Stator voltage, kV Cooling gas temperature, °C up to 40 41-45 46-50 51-55
2) the current in the stator winding should be no more than 1.1 7NOM;
This problem is solved by reconstructing the damper winding of the rotor and significantly reducing the resistance of the contacts between the rotor elements by silvering them.
In the stator winding, losses depend on the height of the conductor and the depth of current penetration into the thickness of the conductor h: (ШЗ) where p is the resistivity of the material; μ—magnetic permeability; o>v is the angular frequency of harmonic eddy currents.
The decrease in generator power due to additional heating of the stator winding by higher harmonics of the current is determined by the additional losses in the copper of the stator winding
14) where Рм - losses in the stator winding, determined by the winding resistance at direct current; ARM - additional losses from higher current harmonics; lv—harmonic current of v-ro order; kf is the displacement coefficient of the fundamental harmonic current.
14) in the upper rods of the winding, where these losses are many times higher than the losses in the lower rods due to the strong displacement of the higher harmonic current.
It is assumed that before the start of the overload, the reactor winding had a steady value of the temperature rise QI < 9Add at current /j < /add. When overloading, the current increases to a value of 1„ and the temperature rise is determined according to the well-known law
24) where t is the time from the beginning of the overload; T—winding heating time constant; 0P is the steady-state value of the temperature rise of the winding at current /„.
The temperature rise of the winding should not exceed the permissible value.
At air temperatures below + 35 °C, the temperature rise of the winding can be increased.
14. General conclusions on the choice of the number and power of power transformers.
6.6. General conclusions on choosing the number and power of power transformers
The choice of the number, power and type of power transformers (autotransformers) for powering the loads of industrial enterprises is made on the basis of calculations and justification according to the general scheme outlined below.
1. The number of transformers at the substation is determined based on ensuring power reliability, taking into account the category of consumers.
2. Outline possible options for the rated power of the selected transformers, taking into account their permissible load in normal mode and permissible overload in emergency mode.
By (6.17) - (6.23)
3. Determine an economically feasible solution from the identified options, acceptable for these specific conditions.
4. Taking into account the possibility of expansion or development of the substation, they decide on the possible installation of more powerful transformers on the same foundations or provide for the possibility of expanding the substation by increasing the number of transformers.
15. Selection of voltages. Determination of rational stress by analytical calculation.
16. Cartogram of loads. Load spread.
17. Electrical Load Center (ELC). Selecting the location of the power source.
18. Decomposition of the load dispersion indicator into components.
19. The problem of the optimal distribution of electrical power receivers of an object among power sources.
20. About the number of power sources. Load distribution connection indicator.
21. Tensor nature of the characteristic properties of load distribution.
22. Indicators of the characteristic properties of a group of receivers.
23. Generalization of the load dispersion tensor.
24. Characteristics of the TsEN scattering zone.
25. Algorithm for constructing the TsEN scattering zone.
26. Determination of the location of supply substations, taking into account the third coordinate.
27. Probabilistic-statistical method for studying the scattering zone of the central heating element.
28. Determination of zones of increase in the reduced annual costs when the substation is displaced from the dispersion zone of the central power plant.
29. Determination of the location of the GPP (GRP), taking into account the development of power supply systems for industrial enterprises.
30. Typical power supply diagrams for industrial enterprises.
31. Maximum permissible heating temperatures of wires and cables. Long-term permissible current load of wires and cables for heating.
CHAPTER 3. PARAMETERS AND EXCHANGE DIAGRAMS OF TRANSFORMERS AND AUTOTRANSFORMERS
3.1. GENERAL INFORMATION AND CHARACTERISTICS
Electricity transmission over long distances is mainly carried out at high voltage (35-750 kV). Electricity distribution is carried out using 6-35(110) kV networks. Electricity consumers are connected to lower voltage networks (0.22-10 kV). For appropriate transformations of voltages, as well as connection of electrical networks of different voltage classes and distribution of electricity, power transformers and autotransformers of single-phase and three-phase versions are used.
At substations of electrical networks and power plants, three-phase two- and three-winding transformers and autotransformers are mainly used. At high power, single-phase transformers are used, connected into three-phase groups.
The symbols of step-down and step-up transformers and autotransformers in the diagrams of electrical power supply systems are shown in Fig. 3.1.
Rice. 3.1. Symbols of transformers and autotransformers in the diagrams: a, b - two-winding unregulated; c - adjustable; g - three-winding adjustable; d - autotransformer; f and g - adjustable and unregulated two-winding transformers with a split low-voltage winding.
The arrows indicate the electrical load S1 and S2 on the buses (terminals) of the highest voltage U1 and low voltage U2 of two-winding transformers (Fig. 3.1, a, b, c). In the case of three-winding transformers and autotransformers, the arrows indicate electrical loads S1, S2 and S3 on the buses of the highest U1, average U2 and lowest U3 voltages (Fig. 3.1, d, e).
The other arrow symbolizes the presence of on-load voltage regulation (OLV). The absence of one means that the transformer is equipped with a device for changing (improving) the PCB voltage (switch without excitation). The voltage change is carried out when the transformer is disconnected from the network.
Schematic diagrams of two- and three-winding transformers are presented in Fig. 3.2 and 3.3.
Rice. 3.2. Connection diagrams for transformer windings: star-star (a), star-delta (b) and corresponding vector voltage diagrams
The high voltage (HV) windings of 6-35 kV two-winding transformers are connected in a star (with an isolated or derived zero point), and the low voltage (LV) windings of 0.4/0.23 kV and 0.69/0.4 kV are connected in a star with a derived zero point, i.e. a group of compounds Y/Yo—0 (Fig. 3.2, a).
At higher winding voltages (VN 110, 150, 220 kV), the LV winding (6-10 kV) is connected into a triangle, which corresponds to the group of connections ΥN/Δ-11 (Fig. 3.2, b).
Rice. 3.3. Connection diagrams for the windings of a three-winding star-zero-star-delta transformer (a) and the corresponding vector voltage diagrams (b)
Rice. 3.4. Connection diagrams for autotransformer windings (a)
and corresponding vector voltage diagrams (b)
In three-winding transformers (HV 110, 150, 220 kV), the HV and MV windings are connected respectively in a star with a removed and isolated zero point. The LV winding at voltages of 6, 10, 20 kV is connected in a triangle, which corresponds to the group of connections YH / Y/Δ - 0/0/11 (Fig. 3.3).
In autotransformers (VN 150, 220, 330, 500, 750 kV) the common windings are connected in a star with mandatory solid grounding of the neutral (Figure 3.4)
The choice of connection diagram for the windings of transforming devices is determined by the neutral mode of the connected networks. A star connection facilitates the insulation of windings exposed to phase voltage; a delta connection is necessary to ensure quality voltage indicators as a result of suppressing the third harmonic of the phase voltage.
The electrical industry produces a large number of standard sizes of three-phase and single-phase power transformers, distinguished by power, rated voltage, number of windings and cooling method. The type of transformer has a symbol that can be used to determine the number of phases, the cooling system, the number of windings, the presence of a control device, the lightning resistance of the transformer insulation, the rated power and the voltage class of the HV winding.
Letter designations of transformers: TM, TS, TSZ, TD, TDTs, TMN TDN, TC, TDG, TDTG, OTs, ODG, ODTG, ATDTsTNG, AOTDTSN, etc. The first letter indicates the number of phases (T - three-phase, O - single-phase ); This is followed by the designation of the cooling system: M - natural oil, i.e. natural circulation of oil; C - dry transformer with natural air cooling, open design; D - oil with blowing, i.e. with blowing into the tank using a fan; C - forced circulation of oil through the water cooler; DC - forced oil circulation with blast. The letter P after the number of phases in the designation indicates that the low voltage winding is represented by two (three) windings (split). The presence of the second letter T means that the transformer is three-winding; two-winding does not have a special designation. The following letters indicate: N - voltage regulation under load (OLC), absence-presence of switching without excitation (PBB); G - thunderstorm. A - autotransformer (at the beginning of the symbol). The letter designations are followed by the rated power of the transformer (kV-A) and, separated by a fraction, the rated voltage class of the HV winding (kV). In autotransformers, the voltage class of the MV winding is added in the form of a fraction. Sometimes the year of production of transformers of this design began is indicated.
The scale of rated power of three-phase power transformers and autotransformers (current state standards 1967-1974) of high-voltage networks is constructed so that there are power values that are multiples of ten: 20, 25, 40, 63, 100, 160, 250, 400, 630, 1000 , 1600 kV*A, etc. Some exceptions are capacities of 32000.80000, 125000, 200000.500000 kV*A.
The standard service life of domestic transformers is 50 years, therefore, in the power supply networks of industrial and agricultural enterprises, transformers manufactured before 1967 and updated due to major repairs can also be used. Their rated power scale: 5, 10, 20, 30, 50, 100, 180, 320, 560, 750, 1000, 1800, 3200, 5600,…, 31500,
40500, kV*A. etc.
Examples of transformer type designations:
TM-250/10-three-phase two-winding with natural oil cooling, voltage change using a PPV device, rated power 250 kV*A, HV winding voltage class 10 kV.
TDTN-25000/110 - three-phase three-winding step-down transformer, oil-cooled with blowing, with on-load tap-changer, rated power 25,000 kV*A, HV winding voltage class 110 kV.
OTs-533000/500 - single-phase two-winding step-up transformer, oil cooling with forced oil circulation, power 533000 kVA, connected to a network with a voltage of 500 kV (nominal phase voltage of the transformer 525/l/3).
ATDTsTN-250000/500/110-85-three-phase three-winding autotransformer, oil cooling with blast and circulation, with on-load tap-changer, rated power 250 MVA, step-down, operating according to an autotransformer circuit between 500 kV and 110 kV networks (HV-MV transformation, LV winding is auxiliary), design 1985
TDTTG-120000/220/110-60 is a three-phase three-winding transformer, the main mode of which is step-up (A), with LV-HV and LV-MV transformations, designed in 1960.
Power transformers and autotransformers are characterized by the following catalog (passport) data: S,,0M - rated power of the transformer, kV*A; UH0M—nominal phase-to-phase (line-to-line) voltages of connected networks; ΔРК—short-circuit active power loss, kW; ΔРХ — active idle power loss, kW; UK - relative value of short circuit voltage, %; IX is the relative value of the no-load current, %.
The ability to regulate and change the voltage is determined by the parameters of the on-load tap-changer and tap-changer. Their characteristics are specified in the form of the maximum number of positive and negative regulatory branches relative to the main terminal of the HV or MV winding, indicating the step of the transformation ratio ΔKt in the form ±nxΔKt. For example, for on-load tap-changer: ±6×1.5%, ±8×1.5% ±10×1.5%, ±9×1.78%, ±12×1%; for PBB: ±2×2.5%.
Rated transformation ratio - the ratio of the rated voltage of the transformer windings:
Changing the transformation ratio is achieved by changing the number of taps (turns) on one of the windings. For transformers with voltage regulation, in particular on-load tap-changers, the transformation ratio must correspond to the actual position of the switch for its nth branch:
For example, with U1 = UHH = 115 kV, U2 = UHH = 11 kV and on-load tap-changer with parameters ±10×1.5%, the number of turns on the HV side changes from WHM to WNB, while the CT changes from KNM to CBN.
The transformation coefficient in the general case is determined by a complex number:
(3.1)
where m is the number of the group of connections of the transformer windings, which determines the phase shift of the low voltage in no-load mode.
For three-winding transformers, in addition to the above parameters, indicate the percentage of the rated powers of the HV, MV and LV windings. For example, modern transformers have windings of equal power, i.e. 100/100/100%, and transformers manufactured before 1967 are characterized by three types of ratios: 100/100/66.7%, 100/66.7/100 %, 100/66.7/66.7%. Autotransformers predominantly have a power ratio of 100/100/50%.
Based on the specified catalog data, all design parameters of equivalent circuits of transforming devices are determined: resistance, conductivity, transformation ratios. These parameters affect power and electricity losses, voltage deviations among electrical consumers and therefore must be taken into account when calculating and analyzing operating modes of electrical networks.
3.2. DOUBLE WINDING TRANSFORMERS
When calculating the modes of three-phase electrical networks with uniform loading of the phases, transformers in the design diagrams are represented by an equivalent circuit for one phase.
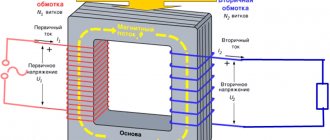
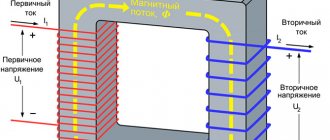
Let us establish a connection between the equivalent circuit of the transformer and its real circuit-mode parameters. The transformer windings are located on a common magnetic core. Therefore, the circuit consists of circuits of primary and secondary windings connected by mutual induction (Fig. 3.5). The presence of magnetic coupling between the windings makes it difficult to study the operating modes of the transformer and the electrical network as a whole. Therefore, in calculations it is convenient to replace this connection with an electrical one. In this case, the analysis of modes is simplified and reduced to calculations of a relatively simple electrical circuit. This circuit, in which the magnetic coupling between the windings is replaced by an electrical one, is called a transformer equivalent circuit. This scheme is based on the idea that the effect of scattering fluxes Фσ1 and Фσ2
is equivalent to the action of the inductive reactances of the windings X1 and X2, through which currents flow, I1 and I2.
In accordance with this, the transformer can be represented as a diagram in Fig. 2.5, a.
Here, each of the transformer windings is replaced by a coil having active and inductive resistance of the actual winding, and magnetically coupled windings with transformation K = W1/W2 without leakage fluxes and without active resistance.
Fig.3.5. Equivalent circuit for two-winding transformers:
a - equivalent circuit of individual windings; b - equivalent circuit of the windings of the reduced transformer; c — T-shaped equivalent circuit
If you bring the secondary winding to the primary winding taking into account the transformation k = W1/W2 (Fig. 3.5, b)
then, as a result, the EMFs E1 and E'2 will be balanced, which makes it possible to combine the windings CD and cd into one, called the magnetizing branch of the equivalent circuit (Fig. 3.5, c).
As a result, a T-shaped circuit was formed, which is the most accurate equivalent circuit for a two-winding transformer (Fig. 3.5, c).
The scheme has longitudinal and transverse elements. The longitudinal elements are represented by active and inductive resistances of one phase of the primary winding Ri and X1 and the secondary winding R'2 and X'2.
The transverse branch, the magnetization branch of the transformer, is presented in the form of active GT and inductive W conductivities, which determine the active Ia and reactive Iμ components of the magnetizing current IX of the transformer. The active component of the current is determined by the power losses in the transformer steel, the reactive component determines the magnetizing flux of the mutual induction of the transformer windings.
The T-shaped equivalent circuit is inconvenient for performing electrical calculations of networks, since even when feeding just one load through a two-winding transformer, the circuit consists of two circuits. Therefore, when calculating the modes of electrical networks, two-winding transformers are replaced with sufficient accuracy by simpler L-shaped equivalent circuits (Fig. 3.6) - direct and reverse, depending on the connection of the conductivity branch (Fig. 3.6, a, b).
In this circuit, the magnetization branch, in contrast to the T-shaped circuit, is usually connected from the primary side, i.e., from the one from which the transformer receives electricity from the source (direct circuit): for step-down transformers - from the HV side, for step-up transformers - from NN. Sometimes, to partially compensate for the error introduced by the use of an L-shaped circuit, as well as during reverse operation of a power transmission, one of the transformers, for example, a step-down one, is turned on in a direct circuit, and the second in a reverse circuit (Fig. 3.7).
The active and reactance of the circuit are equal to the sum of the resistances of both transformer windings reduced to the same voltage. If the circuit is reduced to the highest voltage, the resistance of the windings (through resistance) of the transformers (Fig. 3.7) is determined as
(3.2)
where Z 2 is the total resistance of the secondary winding of the transformer, reduced to the primary voltage.
Rice. 3.6. Various displays of L-shaped equivalent circuits of a two-winding transformer: a - direct circuit; b - reverse diagram
Rice. 3.7. Electric transmission equivalent circuit with direct line
and reverse L-shaped equivalent circuits of step-down and step-up transformers, respectively
If the circuit is reduced to the lowest voltage, then
(3.3)
These total winding resistances are usually called the resistances (active and inductive) of the transformer.
Active conductivity GT is caused by losses of active power in the steel of the transformer due to magnetization reversal (hysteresis) and eddy currents, reactive conductivity W is the power magnetizing the steel. Since the presence of these conductivities is associated with no-load currents IХ (mainly magnetizing current), in approximate calculations in an L-shaped equivalent circuit the conductivity (magnetization branch) of the transformer is replaced by a constant load
equal to the no-load power loss of the transformer (Fig. 3.8, a).
The first term ΔРХ is the active power loss in the transformer steel, a rated value; the second is the magnetizing power of the transformer, taken equal to
(3.4)
where Ix is the no-load current of the transformer with rated power SН0M.
The use of an equivalent circuit, where the magnetization branch is replaced by the power of no-load losses, is permissible at voltages up to 220 kV inclusive.
When calculating the modes of local (distribution) networks of 6-35 kV, the influence of transformer conductivities is neglected and the simplest equivalent circuit is used, consisting only of series-connected active and inductive resistances (Fig. 3.8, b).
In technical and economic calculations related to the calculation and analysis of electricity losses in distribution networks, no-load power losses must be taken into account, since they are comparable to load losses [30, 31].
Rice. 3.8. Simplified equivalent circuits for two-winding transformers: a - taking into account and b - excluding the transverse branch
In the equivalent circuits (Fig. 3.6-3.8), an ideal transformer is included that does not have resistance, but only shows the presence of transformation, that is, the conversion (decrease or increase) of the alternating current voltage of one voltage class to another.
Quantitatively, the value of such a transformation is characterized by the ratio of voltages at the transformer terminals in no-load mode:
(3.5)
Such diagrams are used when calculating the modes of electrical networks, taking into account their actual voltages.
If networks connected by transformers are considered, the parameters of which are reduced to the same voltage class, then the ideal transformer is not taken into account.
The parameters of the equivalent circuit of two-winding transformers are determined from catalog data compiled from the results of open-circuit and short-circuit experiments.
The active and reactive resistances of one phase of the transformer are determined based on the results of a short circuit experiment. A short circuit is the operating mode of a transformer in which the primary winding is connected to the network, and the terminals of the secondary winding are short-circuited (voltage U2 = 0). A short circuit at the rated primary voltage is an emergency mode in which the currents in the windings exceed the rated ones by 10-15 times, and is dangerous for the transformer.
The short circuit experiment is carried out according to the scheme shown in Fig. 3.9, a.
The voltage supplied to the transformer smoothly increases from zero to a value at which the currents in both windings of the transformer are equal to the rated ones. This is the short-circuit voltage Uk, and is usually expressed as a percentage of the rated voltage:
(3.7)
and is about 3-13% for power transformers.
The wattmeter W shows the active power losses ΔРК in the windings and in the steel of the transformer. Losses in steel are insignificant due to the smallness of the applied voltage UK, and in the short circuit experiment all losses of active power are almost entirely spent on heating its windings and can be equated to the nominal losses in the windings of the transformer ΔРК ≈ ΔРН0М. Therefore, it can be accepted with an accuracy sufficient for engineering calculations that in the short circuit experiment
(3.6)
Taking the power loss in kilowatts (kW), the voltage in kilovolts (kV), and the rated power of the transformer in megavoltamperes (MV*A), we obtain the resistance, Ohm,
(3.8)
Or, moving on to power losses in three phases ΔРК = ЗΔРкф, linear voltage UNOM = √3UФНОМ and rated power of a three-phase transformer SNОМ = 3SFНОМ we define the active resistance of the windings of a two-winding transformer , Ohm in the form
(3.9)
Rice. 3.9. Schematic diagrams of short circuit (a) and open circuit (b) experiments on a two-winding transformer (in relation to one phase)
The inductive reactance of the transformer Xt is determined by the short circuit voltage UK. From (3.6) we can determine the total resistance of the transformer, Ohm,
(3.10)
Reactance of transformer windings
(3.12)
For transformers with sufficiently high power (above 1000 kV*A) XT»RT, i.e. the resistance triangle degenerates into a straight line. Therefore, for powerful transformers we can accept with sufficient accuracy
(3.11)
If the short circuit voltage is expressed in relative units pshshiv for the basic nominal parameters of the transformer, we obtain
(3.13)
or, when multiplying expression (2.12) by the factor SNOM/U2NOM with dimension Ohm-1, we have
(3.14)
Thus, the short circuit voltage characterizes the internal resistance of the transformer, which affects the voltage drop and short circuit current.
In the equivalent circuit, resistances RT and CT do not depend on CT, although in reality there is such a dependence.
When transferring a transformer to operate from the main branch to any other, its resistance changes slightly, and therefore in some cases it can be considered unchanged. However, if the CT (and, accordingly, the number of turns of the windings) changes significantly, the resistance of the transformers is calculated for the actual position of the switch.
The conductivity of the equivalent circuit of the transformer is determined based on the results of the no-load test.
The idle test is performed according to the diagram in Fig. 3.9, b. The rated voltage is supplied to the primary winding (with the secondary open). The readings of the wattmeter W determine the total losses of active power in the primary winding and the steel magnetic core of the transformer. Since the no-load current is very small (ranges from 0.7 to 3.0% of the rated value), power losses in the active resistance of the primary winding are negligible. Using an L-shaped equivalent circuit, all no-load losses are, as it were, transferred to the steel core, and losses in steel, with a small error, are equated to the total no-load losses: ΔРСТ = ΔРх. For one transformer phase
(3.15)
From here, moving on to the parameters of a three-phase transformer, we get
(3.16)
Since the idle power loss ΔРСТ is measured in kilowatts, the voltage UNOM is in kilovolts, formula (3.16) takes the following form (GT in Ohm-1)
(3.17)
The active component of the no-load current, reflecting losses in the steel magnetic circuit, is 5-7 times less than the reactive component. If we approximately take the reactive component equal to the entire no-load current: 1C = 1X, then we can determine the reactive conductivity W of the magnetization branch from the following relationship:
(3.18)
Whence, similar to expression (3.17), the reactive conductivity of the magnetization branch of the transformer, Cm, is determined in the form
(3.19)
where Ix is no-load current, %; SH0M is the rated power of the transformer, kVA.
In the calculated expressions for resistance and conductivity, the rated voltages are taken in accordance with what voltage (highest or lowest) the parameters of the transformer equivalent circuit must be reduced to. When calculating the modes of electrical networks, the rated voltage of the transformer winding that is directly connected to the line is taken as the design voltage. Resistances RT, XT, referred to the highest voltage, will have values (UBH/UHН)2 times greater, and conductivities W, GT (UBH/UHH)2 times less than if the equivalent circuit of the transformer were reduced to the lowest voltage.
The rated values of power SH0M, power losses ΔРК, ΔРХ, voltages UH0M, UK, and current IХ are given in the transformer passport: for single-phase - by phase values, for three-phase - by the total power of three phases, phase-to-phase voltages and phase current values.
3.3. THREE WINDING TRANSFORMERS
At step-down substations supplying electrical networks of 10 (6) and 35 kV, three-winding transformers with transformations of 110-220/35/6-10 kV are installed. Electrical networks with a voltage of 10 or 6 kV are designed to supply power to nearby consumers (distance up to 10-15 km). 35 kV networks can supply loads within a radius of up to 40-60 km. If the loads of these networks are comparable (i.e., the difference is no more than 4-5 times), it may be economically feasible to use a three-winding transformer with two secondary windings (Fig. H.10, a)
instead of two-winding 11O-220/6-10 and 11O-220/35 kV (Fig. 3.10,
b)
for separate power supply of distribution networks.
In recent years, domestic three-winding transformers have been manufactured with HV, MV and LV windings of the same power (100%). Previously, three-winding transformers were produced in which the LV and MV windings could have a power 1.5 times less than the power of the HV winding (100/1.5 = 66.7%).
The equivalent circuit of a three-winding transformer of one phase represents a three-rayed star (Fig. 3.11). The parameters of this circuit are active RB, RC, RY, and inductive XB, XC ,
XH, resistances of the HV, MV, LV windings are reduced to the voltage of the primary winding of the transformer. The magnetization branch is connected at the primary terminals of the transformer equivalent circuit. Its parameters are determined in the same way as for two-winding transformers using formulas (3.17) and (3.19).
Rice. 3.10. Schemes of substations with three rated voltages: a - three-winding transformer; b - two two-winding transformers
Rice. 3.11. Equivalent circuits for a three-winding transformer:
a - taking into account and 6 - without taking into account transformation
In accordance with this equivalent circuit for a three-winding transformer, in contrast to a two-winding one, it is necessary to determine the resistance of each winding separately based on short-circuit experiments.
In this experiment, one of the windings is connected to the power source, the second is short-circuited, and the third is open (Fig. 3.12). This allows, when calculating resistance, to consider the equivalent circuit of a three-winding transformer as two series-connected beams. In short-circuit experiments, active power losses ΔРКв-н, ΔРКв-с, ΔРКс-н and short-circuit voltage UKв-с, UKв-н, Uкс-н for each pair of windings (beams of the equivalent circuit) are measured. So, for example, when the MV winding is short-circuited and the transformer is turned on through the HV winding (Fig. 3.12, a)
you can measure power losses ΔРКв-s and short-circuit voltage UКв-н.
Similarly, from experiments for the other two pairs of windings (Fig. 3.12, b, c),
the corresponding power losses and short-circuit voltage are determined.
The results of short circuit experiments allow us to form systems of linear equations of the following form:
(3.20)
(3.21)
Solving equations (3.20) for ΔРКВ, ΔРКС, ΔРКН, we obtain:
(3.22)
Similarly, from systems of equations (3.21) we find:
(3.23)
In the general case, the active and reactance of the windings of three-winding transformers is determined using the same formulas of the form (3.9) and (3.12) as for two-winding transformers.
Reactance Xc
or X„, corresponding to a winding located between two other windings, due to their mutual influence, usually has a value close to zero or a small negative value and in practical calculations is taken equal to zero.
To determine the values of uKB, uKC, uKH, catalogs for three-winding transformers always indicate three normalized (reduced to rated power) values of short-circuit voltage and one (DRK or DRK) or three values of short-circuit losses (DRK, DRK, DRV) depending on transformer type.
If short circuit losses are specified for one pair of windings, then the active resistances can be found under the assumption that these resistances, reduced to one transformation stage, are inversely proportional to the rated powers of the corresponding windings. Rice. 3.12. Schemes of three short-circuit experiments of a three-winding transformer
For transformers with the same winding powers, the total short circuit losses per pair of windings are equally distributed between the corresponding windings, i.e. in this case, the active resistance of the equivalent circuit beams is calculated using the formula
(3.24)
If in a three-winding transformer one of the windings has a power less than the rated one (ratio S,H/SC1,/SH1, = 100/100/66.7% or 100/66.7/100%), then the active resistance of the equivalent circuit beams for windings with a rated power of 100% are determined similarly to the previous case:
R100=- (3.25)
The value of the active resistance of the equivalent circuit beam of the corresponding winding with a lower power (66.7%), reduced to the rated power of the transformer, is found taking into account the inverse proportionality of the resistances and powers of the windings:
from where (3.26)
Transformations from higher to medium and lower voltages are taken into account (Fig. 3.11, a)
corresponding ideal transformers with parameters
(3,27)
Calculation of the modes of electrical networks reduced to one rated voltage is carried out taking into account the equivalent circuit shown in Fig. 3.11, b.
3.4. AUTOTRANSFORMERS
Along with transformers, autotransformers are widely used to connect networks and their elements with different rated voltages.
An autotransformer is a multi-winding transformer in which two windings are connected magnetically and electrically. It is most economically feasible to use autotransformers for connecting networks with solidly grounded neutrals with voltages of 110 kV and higher with a rated voltage ratio of up to 3-4, for example, 220 and 110 kV, 500 and 220 kV, etc. Three-winding autotransformers have been used in power systems - three-phase and single-phase, assembled into three-phase groups.
In Fig. Figure 3.13 shows a diagram of the connections of the windings of a three-winding autotransformer. High voltage winding (HV) 1 consists of two windings - common and series. The medium voltage (MV) winding 2 is part of the HV winding and is called the common winding, and the rest of the HV winding is called the series winding. The third winding 3 is a low voltage (LV) winding and is connected to the other windings only magnetically.
Let's consider the operating conditions of a step-down three-winding autotransformer (Fig. 3.13). Autotransformers can operate in autotransformer and combined modes. When operating in autotransformer mode, power will be transferred from the HV network to the MV network or vice versa. The LV tertiary winding is not loaded. When operating in combined mode, a load or compensating devices are connected to the LV winding of the autotransformer. In this case, the power in the series and common windings consists of the power transmitted in autotransformer mode and the power transmitted through the LV winding.
Unlike a transformer, where all the power from the primary winding of the high voltage voltage is transferred to the secondary winding of the medium voltage by a magnetic field, in an autotransformer part of the power is transmitted directly - without transformation, through an electrical (contact) connection between the series and common windings (electric power):
(3,28)
Rice. 3.13. Schematic diagrams of three-winding autotransformers: a - single-phase; b - three-phase group of autotransformers
and also with the help of the magnetic flux penetrating them, i.e. magnetically (transformer power)
(3.29)
The sum of the transformer and electrical powers is equal to the throughput power of the autotransformer:
(3.30)
The rated power of an autotransformer is understood as the maximum power that can be transmitted through an autotransformer along the HV and MV windings, which have an autotransformer connection with each other. For domestic autotransformers, the power of the HV and MV windings is the same and equal to the nominal or throughput. Hence,
(3.31)
The difference between the currents of the HV and MV networks flows in the common winding. Therefore, this winding is designed for a current less than the rated current of the autotransformer, determined on the HV side, and it may have a smaller cross-sectional area than the winding of the same voltage of a two-winding transformer. The magnetic circuit of the autotransformer also has a smaller area. As a result, the closer to unity the transformation coefficient
the lower the consumption of active materials (copper windings, magnetic core steel and insulating materials) and approximately the cost of the autotransformer. Therefore, step-down autotransformers are cheaper than transformers of equal rated power, and the use of autotransformers instead of a transformer