Basic parameters of conductor materials. Dependence on conductor composition and external factors

The main indicators of the properties of conductor materials, regardless of their application, include: 1 - electrical resistivity; 2—temperature coefficient of resistivity; 3 —

thermal conductivity;
4—contact potential difference and thermoelectromotive force (thermo-EMF); 5—work function; 6 -
tensile strength σр and relative elongation at break, etc.

a) Electrical resistivity of conductive materials

Under electrical resistivity

understand the resistance of a cube with an edge of 1 m, cut from the material under study, if the current passes through two opposite faces of this cube. The SI unit of resistivity is Ohm*m. In addition to the SI unit - Ohm * m, in practice they often use the non-system unit Ok * mm2 / m or equal in size - μOhm * m. The connection between them is expressed as

1 Ohm*m = 106 μOhm*m = 106 Ohm*mm2/m.

The range of resistivity values of metal conductors at normal temperature is quite narrow: from 0.016 μΩ*m for silver and to approximately 10 μΩ*m for some alloys, i.e., it takes only three orders of magnitude.

Based on the resistivity value, conductive materials are divided into high conductivity materials with

specific electrical resistance ρ, at normal temperature no more than 0.1 μOhm*m and
high-resistance materials with
ρ at normal temperature not less than 0.3 μOhm*m.

A special group is represented by superconducting and cryo-conducting

materials. These include materials that at low (cryogenic) temperatures have a vanishingly small value (close to zero for superconductors) of electrical resistivity.

Highly conductive materials, and these are primarily metals, are used in the production of radio wiring, conductive cable cores, solders, thin-film contact coatings in microcircuits, etc. Highly conductive conductive materials that have the greatest practical application in radio electronics include copper

and
aluminum.
The electrical resistivity of copper is 0.0172 μOhm*m. Copper is an expensive and scarce material, and is often replaced with aluminum (p = 0.028 μΩ*m).

High-resistance alloys are used in the manufacture of wire-wound and thin-film resistors, electric heating elements, rheostats, etc. The main representatives of this group of conductor materials are manganin and constantan.

b) Dependence of electrical resistivity of conductor materials on temperature

The electrical resistivity of conductors increases with increasing temperature. This is due to the fact that with increasing temperature, vibrations of crystal lattice nodes intensify and the probability of electron waves being scattered by them increases, which leads to a decrease in the mean free path and mobility of electrons.

Near absolute zero, the scattering of electron waves by thermal vibrations of the lattice tends to zero, but scattering by lattice defects has a finite value and thereby determines the presence of residual resistance.

According to the empirically established Matthiessen rule, the resistivity of a metal conductor can be expressed by the formula

ρ = ρо+growth, (12.1)

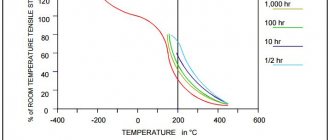
where po is the resistivity component, depending only on temperature; ρres – the residual component of resistivity, which does not depend on temperature and is a quantitative measure of the degree of structural perfection of the crystal lattice. A typical curve of changes in the resistivity of a metal conductor depending on temperature is shown in Fig. 12.1. At low (cryogenic) temperatures (in region 1), the value of p is practically independent of temperature and is determined mainly by the value of the residual resistance, which is smaller, the purer and more perfect the metal. In conductive metals of high conductivity, having a resistivity of no more than

Fig. 12.1 Changes in the resistivity of a metal conductor depending on temperature
0.1 μOhm*m, the content of impurities is limited to tenths, hundredths and even thousandths of a percent. For the manufacture of rheostats, resistors, and electric heating elements, not metals are used, but high-resistance alloys with increased growth rates. As a rule, alloys that are solid solutions have the greatest growth value. In hard metals and alloys subjected to cold drawing and drawing, the resistivity increases as a result of distortion of the crystal lattice. Soft annealed metals and alloys restore the structure distorted during recrystallization and their resistivity decreases.

The increase in resistivity with temperature in regions II and III is associated with electron-phonon interaction, and thermal vibrations of the crystal lattice at temperatures below the Debye temperature ΘD are qualitatively different from vibrations at T>

ΘD
,
which explains those shown in Fig.
12.1 dependencies. In region II at T <
ΘD, the change in the resistivity of conductor materials with temperature is determined by a change in the frequency spectrum of vibrations of the crystal lattice nodes, i.e.
the emergence of more and more new frequencies of thermal vibrations of the lattice, the maximum of which is determined by the Debye temperature. In this region, ρ ~Tn,
where
n
varies from 5 to 1. In region III at T> ΘD, the change in electrical resistivity occurs almost linearly and is explained by a linear increase in the amplitudes of vibrations of crystal lattice nodes with temperature.

For most metals, the Debye temperature ΘD lies in the range from 100 to 500 K; for aluminum, for example, it is 418 K.

In region IV, a deviation of the dependence of the electrical resistivity from linear is observed. As a rule, this area is small and located near the melting temperature of the metal. During a phase transition from one state of aggregation to another, the resistivity of metals changes abruptly. When metals melt (region V), ρ usually increases. However, for metals whose density decreases during melting (bismuth, antimony, gallium), the value of electrical resistivity ρ decreases during melting.

In the temperature range where the dependence ρ =f(T)

is close to linear, a linear-piecewise approximation of this dependence is acceptable, and the value of electrical resistivity can be calculated using the formula

ρt = ρо[1+αср (t-t0)] , (12.2)

where ρо, ρt are the resistivity of the material at temperatures -t0 and t, respectively. The value of αср in expression (12.2) (the designation TKr is more often used)

is called the average temperature coefficient of resistivity in a given temperature range:
(12.3)
.. (12.4)

In general, the temperature coefficient of resistance of a material is the logarithmic derivative of this parameter with respect to temperature:

Thus, the temperature coefficient of resistance characterizes the relative resistance of the conductor when the temperature changes by one degree and has a dimension inverse to temperature. The other temperature coefficients have the same physical meaning. Metals have a large temperature coefficient of resistivity (for example, for aluminum TCR in the temperature range from 0 to 150 °C is 4 * 10-3 K-1), for alloys the TCR value is much lower (10-4 – 10-6 K-1 ). Alloys with TKr = 10-5 – 10-6 K-1 are considered materials with constant resistance over a wide temperature range. These include, for example, constantan.

c) Electrical conductivity of thin metal films

In microelectronics, films of conductors used for switching circuit elements have also become widespread. For a comparative assessment of the conductive properties of metal films, the thickness of which d is commensurate with the electron mean free path λ, the parameter of specific surface electrical resistance or squared resistance ρ□, Ohm/□ is used. Specific surface resistance is numerically equal to the resistance of a section of the film, the length of which is equal to its width when current flows through its two opposite faces parallel to the substrate surface:

ρ□= ρ□/4 , (12.5)

where p is the specific (volume) resistance of the film, and d —

its thickness. The specific surface resistance of thin films, as a rule, is greater than the specific resistance of the same metal in thick layers and depends on the thickness of the film and the method of its preparation.

For thin films (d/ λ <1), the ratio of the conductivity γpl to the conductivity of the bulk metal γ is determined by the relation

(12.6) For very thin films (d/ λ <<1) this expression is simplified and has the form:

(12.7)

The given relationships are used for practical calculations and are obtained under the assumption that electron scattering occurs as a result of their interaction with each other and with the surface of the film.

When choosing materials for thin-film elements in microelectronics, the magnitude and sign of the temperature coefficient of resistance TC

ρ.
The TC
of films is, as a rule, less than
the TC
of bulk metals, and for very thin films it can be negative.
The layer thickness at which TC
ρ changes sign depends both on the type of metal and on the film production technology.

c) Conductor resistance at high frequencies

A conductor placed in a high-frequency electromagnetic field is characterized by an uneven distribution of current density over the cross section of the conductor, and the value of the current density is significantly different from zero only in a thin layer near the surface. This phenomenon is called the skin effect

or
surface effect.
The distance from the surface of the conductor at which the current density decreases in e

times compared to its density on the surface, is called
the effective penetration depth of alternating
current and is denoted by Δ:
, (12.8)
where ω is the frequency of the electromagnetic field; λ, μa is the electrical conductivity of the conductor for direct current and its absolute magnetic permeability.

In an ideal conductor, in which γ→ ∞the penetration depth is ∆→0, i.e., complete reflection of electromagnetic waves is observed. The ability of a technical conductor material operating in the high-frequency region to conduct electric current in radio engineering is characterized by the resistance of a square surface

conductor Rs, Ohm.

For a flat conductor of infinite thickness, the value of Rs is determined from an expression similar to (12.6). The difference is that instead of the film thickness, the current penetration depth Rs is taken into account :

Rs = 1/( γ*∆), (12.9)

where γ is the conductivity of the metal. The expression shows that the active resistance of a flat conductor of infinite thickness with the skin effect Rs ,

is equal to the resistance of a flat conductor of thickness ∆ for direct current or, which is the same, the active resistance of a conductor with an exponentially decreasing current density distribution is equal to the resistance of a conductor of thickness ∆ with a uniform current distribution.

e) Superconductivity phenomena

Superconductivity

call the phenomenon of a drop in the value of electrical resistivity (almost to zero; ρ-10-16 Ohm*m) of some materials at a certain temperature, called
the transition temperature
or critical temperature Tcr.

Substances with such properties are called superconductors.

Currently, over a thousand superconductors are known, among them more than 20 pure metals (for example, aluminum, lead, mercury), many alloys and a number of compounds containing non-metals (for example, copper sulfide, molybdenum carbide, etc.).
Superconductors that are pure metals are called soft
superconductors, in contrast to alloys and chemical compounds that are called
hard
superconductors.

In Fig. 12.2 shows the temperature dependences of the electrical resistivity of some superconducting metals and indicates the values characteristic of their critical transition temperature.

Fig. 12.2 temperature dependences of the electrical resistivity of some superconducting metals
In reality, the transition of materials from the ordinary state to the superconducting state occurs in a certain temperature range, the width of which depends on the presence of impurities, defects, and internal stresses in the material. For soft superconductors, this region is small and amounts to approximately 10-3 degrees.

The transition temperatures of superconductors to the superconducting state are low. So, for example, for some pure metals their values range from 0.35 K (hafnium) to 9.2 K (niobium); for alloys - from 0.155K. (BiPt) up to 18K (Nb3Sn).

Achieving such low (cryogenic) temperatures is carried out in special cooling units using refrigerants and is a complex and expensive task. Various liquefied gases are used as refrigerants.

The phenomenon of superconductivity was discovered in 1911 by the Dutch scientist G. Kammerlingh-Onnes while studying the electrical conductivity of a ring of mercury frozen to 4.2 K. However, a satisfactory explanation of the phenomenon of superconductivity was proposed only in 1957 by Bardeen, Cooper and Schiffer. Soviet scientists N.N. Bogolyubov and A.A. Abrikosov made a great contribution to the theory of superconductivity.

The mechanism for the occurrence of superconductivity is as follows. In some materials at low temperatures, the interaction of electrons with the crystal lattice is so strong that forces arise that bind electrons in pairs into so-called Cooper pairs, namely, two electrons located on opposite sides of the nearest positively charged lattice ion are attracted to it by Coulomb attraction forces , and in the presence of an electric field they drift inside the crystal in pairs without dissipating energy. Such pairs exist only at temperatures below a certain critical temperature (quite certain for each superconductor), i.e., when the thermal energy of the system is not enough to break the bonds between electrons. The absence of electron scattering by thermal vibrations of crystal lattice nodes with this mechanism of electrical conductivity leads to the conclusion that a current, once induced in a superconducting circuit, can circulate in it for a long time (about 105 years) practically without attenuation.

The superconducting state can be destroyed not only by increasing temperature, but also by other external influences. Such an influence may be, for example, a high-frequency electric or magnetic field; it makes no difference whether the latter is created by a current flowing through the superconductor itself, or by an external source of a magnetic field.

Rice. 12.3 Phase diagrams of superconductors of the first and second types.

According to the thermodynamic theory of superconductivity, the superconducting and non-superconducting (“normal”) states are two phases of a substance that transform into one another at certain values of state parameters—temperature Tcr

and magnetic field strength.
The value of the magnetic induction at which the material transitions from the superconducting to the normal state is called critical and is designated Vcr. Based on the nature of the transition, superconductors of the first and second kind are distinguished, the phase diagrams of which are shown in Fig. 12.3, a, b,
respectively.
The curve separating the region of the superconducting state from the non-superconducting state is called the boundary
Type I superconductors are characterized by an abrupt change in the state of the substance (its internal energy).

Type II superconductors have an intermediate state in which the superconducting and normal phases exist simultaneously. The values of Vkr1 and Vkr2 can differ by hundreds of times. Superconductors of the second type include solid superconductors, i.e. all alloys, intermetallic compounds, as well as films even from superconductors of the first type, if their thickness is less than the depth of penetration of the magnetic field.

As can be seen from the figures, the highest possible value of the transition temperature of a given superconducting material is achieved only at negligible magnetic induction and vice versa. The problem of increasing the values of these values Vcr and Tcr

is one of the most important problems in the physics and technology of superconducting materials. There are theoretical premises that some organic semiconductor materials will be superconducting at room temperature. However, to date such materials have not been obtained.

In 1933, German physicists W. Meissner and R. Ochsenfeld discovered that superconductors, when transitioning to a superconducting state, become “ideal diamagnets,” that is, their magnetic permeability μ drops abruptly from μ≈1 to μ=0. Therefore, an external magnetic field does not penetrate the superconducting body, and if the transition occurs in a magnetic field, then the field is almost completely “pushed out” of the superconductor.

This effect (Meissner effect)

found application for the manufacture of bearings with “magnetic lubrication”, operating practically without friction with mutual repulsion of the shaft and bearing, for “magnetic suspension” of high-speed railway cars, etc.

Along with this, superconductors have found widespread use in the production of electromagnets. A superconducting electromagnet is a superconducting solenoid flowing around current. Superconducting electromagnets are much cheaper than conventional electromagnets, smaller in size and weight, and consume less energy.

In addition to electromagnets, superconductors are used for the manufacture of windings of electrical machines, transformers and other devices of low mass and size and with high efficiency, cable lines for transmitting high powers, waveguides with low attenuation, energy storage devices, etc. A number of memory control devices are based on the transfer of material from superconducting state to normal when magnetic induction or temperature changes.

Recently, reports have appeared on the observation of the effect of superconductivity in a number of semiconductors, for example, in strontium titanate, where superconductivity was discovered in oxygen-destoichiometric crystals at a carrier concentration of 1018-1021 cm12. The discovery of these materials makes it possible to create fundamentally new devices and systems in microelectronics.

d) Cryoconductors

In paragraph b

It has been shown that the electrical conductivity of metals increases with increasing purity and decreasing temperature. Materials that, from this point of view, have the most advantageous properties, i.e., the greatest change in conductivity when temperatures drop to cryogenic temperatures, are called cryoconductors. The value of the electrical resistivity of cryoconductors in the region of low temperatures (but at temperatures above Tcr, if this material belongs to superconductors) is three to four orders of magnitude less than at normal temperatures. For ordinary metals this change is one order of magnitude. It should be noted that the physical processes underlying the phenomena of superconductivity and cryoconductivity are different. Unlike superconductors, which include many alloys and chemical compounds, only pure metals with the lowest possible concentration of crystal lattice defects are used as cryoconductors.

The best cryoconductor in the temperature range close to the temperature of liquid hydrogen (about 20 K) is pure aluminum, and for the temperature range close to the temperature of liquid nitrogen - beryllium.

The possibility of using cheaper refrigerants: liquid hydrogen and nitrogen compared to liquid helium is one of the main advantages of using cryoconductors compared to superconductors. This simplifies the design and operation of installations, simplifies thermal insulation and reduces energy consumption for cooling. The permissible current densities in cryoconductors are one to two orders of magnitude higher than for conventional conductor materials. This reduces losses in electrical machines, devices, cables, where cryoconductors are mainly used.

Development prospects

Previous34Next

WHAT AND HOW THEY WRITTEN ABOUT FASHION IN MAGAZINES AT THE BEGINNING OF THE XX CENTURY The first issue of the Apollo magazine for 1909 began, in fact, with a policy statement from the magazine’s editors...

Live by the rule: IS THERE NOT MUCH THING IN THE WORLD EXISTING? It is no coincidence that I emphasize that the space in your head is limited, but there is a lot of information around, and that your right...

WHAT IS CONFIDENT BEHAVIOR IN INTERPERSONAL RELATIONSHIPS? Historically, there are three main patterns of differences that exist between...

System of Protected Areas in the USA The study of specially protected natural areas (SPNA) in the USA is of particular interest for many reasons...

Didn't find what you were looking for? Use Google search on the site:

Metal conductor material

GOST 33290-2015 paint and varnish materials used in construction. general technical conditions

Metal conductor materials can be divided into high conductivity materials and high resistance materials. High conductivity materials are used for the manufacture of cables, wires, windings of electrical machines and transformers.

Metal conductor materials are divided into high conductivity materials and high resistance alloys. High-conductivity metals are used in cases where it is necessary to ensure minimal losses of electrical energy transmitted through them, and high-resistance alloys, on the contrary, in cases where it is necessary to transform electrical energy into heat.

All metallic conductor materials exhibit electronic conductivity. The resistivity of all metal conductors increases with increasing temperature, as well as as a result of mechanical processing, which causes permanent deformation in the metal.

The resistance of metallic conductor materials is highly dependent on temperature: it increases with increasing temperature. The degree to which temperature influences resistance is determined by the temperature coefficient.

From metallic conductor materials, high conductivity metals can be isolated, having a resistivity p

A wide range of metal conductor materials are produced for the production of sliding electrical contacts. In table 4.2 and 4.3 show the main characteristics of the most common of these materials, and table. 4.4 - properties of coatings used to improve the characteristics of sliding contact.

The most common conductor materials are metals, primarily copper and aluminum, as well as their alloys. Metal conductor materials are used for the manufacture of conductive elements of electrical equipment of automobiles. In automobile electrical wiring, insulated wires are used, collected in bundles, braided with polyvinyl chloride tape and cotton yarn.

Metal alloys have less ductility compared to pure metals, they are more elastic and have greater mechanical strength. A characteristic feature of all metallic conductor materials is their electronic conductivity. The resistivity of all metal conductors increases with increasing temperature, as well as as a result of mechanical processing, which causes permanent deformation in the metal.

Conductor materials with high resistance are metallic, which is the most common, and non-metallic. Metal conductor materials can be divided into three groups: I - for precision electrical measuring instruments and standard resistors; 2 - for resistors and rheostats; 3 - having a high operating temperature and intended for heating devices and load rheostats.